题目内容
设函数F（x）=
是定义在R上的函数，其中f（x）的导函数f′（x）满足f′（x）＜f（x）对于x∈R恒成立，则 （ ）
| f(x) |
| ex |
| A、f（2）＞e2f（0），f（2012）＞e2012f（0） |
| B、f（2）＞e2f（0），f（2012）＜e2012f（0） |
| C、f（2）＜e2f（0），f（2012）＞e2012f（0） |
| D、f（2）＜e2f（0），f（2012）＜e2012f（0） |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：由f′（x）＜f（x），利用导数与函数单调性的关系，判断出函数F（x）=
是定义在R上的减函数，即可得答案．
| f(x) |
| ex |
解答：
解：由f′（x）＜f（x）得，f′（x）-f（x）＜0，
∴F′（x）=
＜0，
∴函数F（x）=
是定义在R上的减函数，
∴F（0）＞F（2），F（0）＞F（2012），
即F（0）＞
，F（0）＞
，
即f（2）＜e2F（0），f（2012）＜e2012F（0），
∵F（0）=f（0），
∴f（2）＜e2f（0），f（2012）＜e2012f（0），
故选：D．
∴F′（x）=
| f′(x)-f(x) |
| ex |
∴函数F（x）=
| f(x) |
| ex |
∴F（0）＞F（2），F（0）＞F（2012），
即F（0）＞
| f(0) |
| e2 |
| f(2012) |
| ex |
即f（2）＜e2F（0），f（2012）＜e2012F（0），
∵F（0）=f（0），
∴f（2）＜e2f（0），f（2012）＜e2012f（0），
故选：D．
点评：考查利用导数研究判断函数单调性及导数的运算法则的运用，属于中档题，
练习册系列答案
名校课堂系列答案
相关题目
下列各组中的两个函数是同一函数的是（ ）
| A、f（x）=（x-1）0与g（x）=1 | ||||||||
B、f（x）=x与g（x）=
| ||||||||
C、f（x）=
| ||||||||
D、f（x）=
|
已知全集U=R，集合A={x|2x＞1}，B={x|-4＜x＜1}，则A∩B等于（ ）
A、（
| ||
| B、（1，+∞） | ||
| C、（-4，1） | ||
| D、（-∞，-4） |
已知函数y=f（x），对任意的两个不相等的实数x1，x2，都有f（x1+x2）=f（x1）•f（x2）成立，且f（0）≠0，则f（-5）•f（-3）•f（-1）•f（1）•f（3）•f（5）的值为 ．
f（x）=
是定义在（-∞，+∞）上是减函数，则a的取值范围是（ ）
|
A、[
| ||||
B、[0，
| ||||
C、（0，
| ||||
D、（-∞，
|
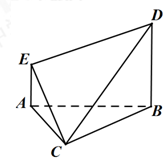如图，在多面体ABCDE中，AE⊥平面ABC，BD∥AE，且AC=AB=BC=BD=2，AE=1