题目内容
11．
已知函数f（x）=$\left\{\begin{array}{l}{x+2，x≤-1}\\{{x}^{2，}-1＜x＜2}\\{2x，x≥2}\end{array}\right.$．（1）求f（f（-2））；
（2）画出函数f（x）的图象，根据图象写出函数的单调增区间并求出函数f（x）在区间（-4，0）上的值域．
分析 （1）利用分段函数求解函数值即可．
（2）画出函数的图象，利用函数的图象写出函数的单调增区间并求出函数f（x）在区间（-4，0）上的值域．
解答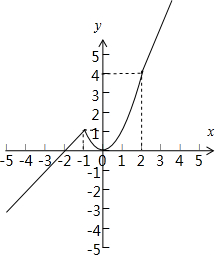 
解：（1）函数f（x）=$\left\{\begin{array}{l}{x+2，x≤-1}\\{{x}^{2，}-1＜x＜2}\\{2x，x≥2}\end{array}\right.$．
f（-2）=-2+2=0，
f（f（-2））=f（0）=0.3分
（2）函数的图象如图：…（6分）
单调增区间为（-∞，-1），（0，+∞）（开区间，闭区间都给分）…（9分）
由图可知：
f（-4）=-2，f（-1）=1，
函数f（x）在区间（-4，0）上的值域（-2，1]．…12分．
点评 本题考查分段函数的应用，函数的图象的画法，二次函数的简单性质的应用，考查数形结合以及计算能力．
练习册系列答案
相关题目
2．已知α是△ABC的一个内角，且$sinα+cosα=\frac{{\sqrt{2}}}{2}$，则sin2α的值为（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | 3 | D． | -3 |
19．某服装商场为了了解毛衣的月销售量y（件）与月平均气温x（℃）之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如表：
（1）算出线性回归方程$\widehat{y}$=bx+a； （a，b精确到十分位）
（2）气象部门预测下个月的平均气温约为6℃，据此估计，求该商场下个月毛衣的销售量．
参考公式：线性回归方程为，其中b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$．
| 月平均气温x（°C） | 17 | 13 | 8 | 2 |
| 月销售量y（件） | 24 | 33 | 40 | 55 |
（2）气象部门预测下个月的平均气温约为6℃，据此估计，求该商场下个月毛衣的销售量．
参考公式：线性回归方程为，其中b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$．
16．若函数f（x）=2sin（ωx-$\frac{π}{3}}$）（0＜ω＜2π）的图象关于直线x=-$\frac{1}{6}$对称，则f（x）的递增区间是（ ）
| A． | $[{-\frac{1}{6}+2kπ，\frac{5}{6}+2kπ}]，k∈z$ | B． | $[{-\frac{1}{6}+2k，\frac{5}{6}+2k}]，k∈z$ | ||
| C． | $[{\frac{5}{6}+2kπ，\frac{11}{6}+2kπ}]，k∈z$ | D． | $[{\frac{5}{6}+2k，\frac{11}{6}+2k}]，k∈z$ |