题目内容
(12分)我们把同时满足下列两个性质的函数称为“和谐函数” :
①函数在整个定义域上是单调增函数或单调减函数;
②在函数的定义域内存在区间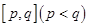 ,使得函数在区间
,使得函数在区间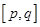 上的值域为
上的值域为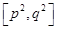 .
.
⑴已知幂函数 的图像经过点
的图像经过点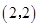 ,判断
,判断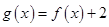
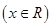 是否是和谐函数?
是否是和谐函数?
⑵判断函数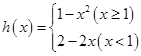 是否是和谐函数?
是否是和谐函数?
⑶若函数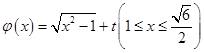 是和谐函数,求实数
是和谐函数,求实数 的取值范围.
的取值范围.
(1)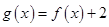 是和谐函数。(2)
是和谐函数。(2) 不是和谐函数。(3)
不是和谐函数。(3) 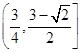 .
.
解析试题分析:. (1)设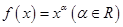 ,由
,由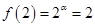 ,得
,得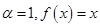 ,
,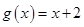 在
在 上是增函数,
上是增函数,
令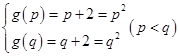 ,得
,得
故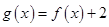 是和谐函数。 ………………………4分
是和谐函数。 ………………………4分
⑵易得 为
为 上的减函数,
上的减函数,
① 若 则
则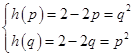 ,相减得
,相减得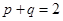 与
与 矛盾;
矛盾;
② 若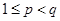 则
则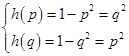 ,
, 与
与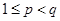 矛盾;
矛盾;
③ 若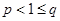 则
则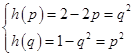 ,
,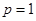 与
与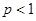 矛盾。
矛盾。
故 不是和谐函数。 ………………………………………8分
不是和谐函数。 ………………………………………8分
⑶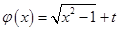 在
在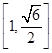 上是增函数,
上是增函数,
由函数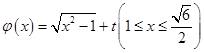 是和谐函数知, 函数
是和谐函数知, 函数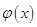 在
在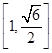 内存在区间
内存在区间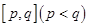 ,使得函数在区间
,使得函数在区间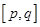 上的值域为
上的值域为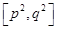 .
.
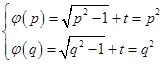
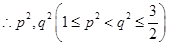 是方程
是方程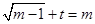 在区间
在区间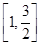 内的两个不等实根
内的两个不等实根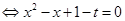 在区间
在区间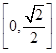 内的两个不等实根,
内的两个不等实根,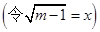
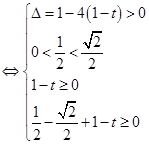
 ………………………12分
………………………12分
考点:函数的单调性;函数的值域;函数的综合应用;一元二次方程根的分布问题。
点评:(1)此题以新定义为背景,来考查函数的综合应用。考查了学生分析问题、解决问题的能力以及分类讨论的数学思想。(2)设一元二次方程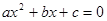 (
(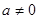 )的两个实根为
)的两个实根为 ,
,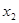 ,且
,且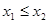 。
。
① 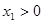 ,
,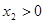 (两个正根)
(两个正根)
 ;
;
②  ,
,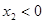 (两个负根)
(两个负根)
 ;
;
③ 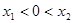 (一个正根一个负根)
(一个正根一个负根)
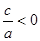 。
。

练习册系列答案
相关题目
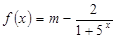 。
。 ,使
,使 是奇函数?若存在,求出
是奇函数?若存在,求出 的值;若不存在,给出证明。
的值;若不存在,给出证明。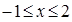 时,
时,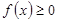 恒成立,求实数
恒成立,求实数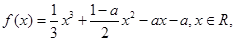 其中
其中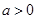 .(1)求函数
.(1)求函数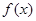 的单调区间;(2)若函数
的单调区间;(2)若函数 内恰有两个零点,求
内恰有两个零点,求 的取值范围;
的取值范围; 时,设函数
时,设函数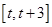 上的最大值为
上的最大值为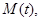 最小值为
最小值为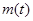 ,记
,记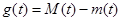 ,求函数
,求函数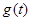 在区间
在区间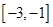 上的最小值.
上的最小值.
 (百件)与销售价格
(百件)与销售价格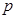 (元)的关系如下图,每月各种开支2000元.
(元)的关系如下图,每月各种开支2000元.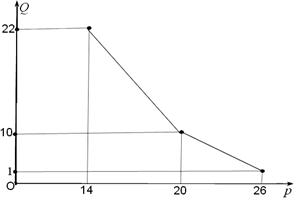
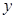 (元)与销售价格
(元)与销售价格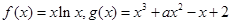
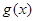 的单调减区间为
的单调减区间为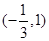 ,求函数
,求函数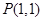 的切线方程;
的切线方程;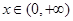 ,不等式
,不等式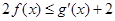 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。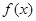
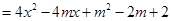 的图像与
的图像与 轴有两个交点
轴有两个交点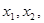 试判断函数
试判断函数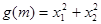 有没有最大值或最小值,并说明理由.
有没有最大值或最小值,并说明理由.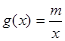 在区间
在区间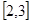 上都是减函数,求实数
上都是减函数,求实数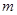 的取值范围.
的取值范围.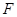 、
、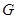 的函数
的函数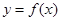 、
、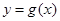 ,
,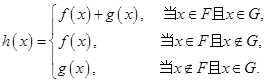
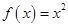 ,
,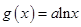
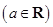 .
.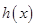 的解析式;
的解析式;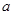 ,函数
,函数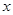 均有
均有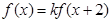 ,其中常数k为负数,且
,其中常数k为负数,且 在区间
在区间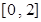 上有表达式
上有表达式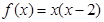
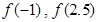 的值;
的值;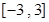 上的表达式,并讨论函数
上的表达式,并讨论函数