题目内容
已知函数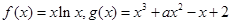
(1)如果函数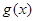 的单调减区间为
的单调减区间为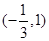 ,求函数
,求函数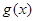 的解析式;
的解析式;
(2)在(1)的条件下,求函数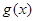 的图像过点
的图像过点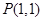 的切线方程;
的切线方程;
(3)证明:对任意的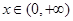 ,不等式
,不等式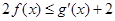 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(1)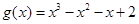 ;(2)
;(2)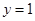 或
或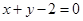 ;(3)
;(3)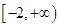
解析试题分析:(1)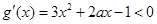 的解集是
的解集是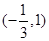 ,所以将
,所以将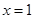 代入方程
代入方程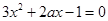
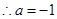 ,
,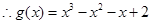
(2)若点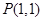 是切点,,则切线方程为
是切点,,则切线方程为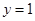
若点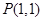 不是切点,,则切线方程为
不是切点,,则切线方程为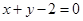
(3)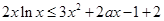 在
在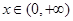 上恒成立
上恒成立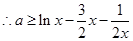
设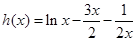 ,
,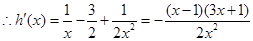
令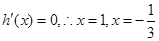 (舍)
(舍)
当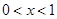 时,
时,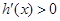 ,当
,当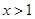 时,
时,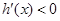
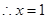 时,
时,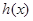 取得最大值,
取得最大值,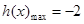
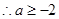
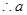 的取值范围是
的取值范围是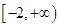
考点:本题考查了导函数的应用、导数的几何意义及函数性质的应用
点评:导数在高考中有着重要的应用,已成为众多交汇的载体,如研究函数的单调性问题,最值问题,参数问题等

练习册系列答案
相关题目
(本小题满分12分)探究函数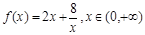 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 16 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
(1)函数
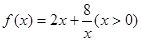 在区间(0,2)上递减;函数
在区间(0,2)上递减;函数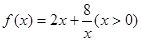 在区间 上递增.当
在区间 上递增.当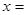 时,
时,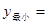 .
.(2)证明:函数
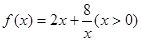 在区间(0,2)递减.
在区间(0,2)递减.(3)思考:函数
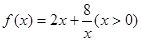 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明) 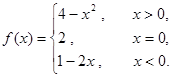
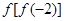 的值;
的值;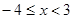 时,求函数
时,求函数 的值域。
的值域。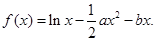
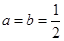 时,求函数
时,求函数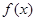 的最大值;
的最大值;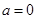 ,
,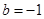 ,方程
,方程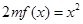 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值.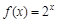 ,
,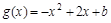
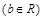 ,记
,记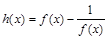 。
。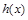 的奇偶性,并证明;
的奇偶性,并证明;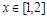 ,都存在
,都存在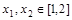 ,使得
,使得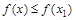 ,
,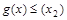 .若
.若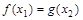 ,求实数
,求实数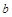 的值;
的值;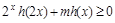 对于一切
对于一切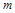 的取值范围.
的取值范围.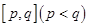 ,使得函数在区间
,使得函数在区间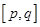 上的值域为
上的值域为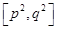 .
. 的图像经过点
的图像经过点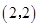 ,判断
,判断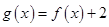
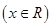 是否是和谐函数?
是否是和谐函数?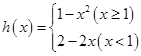 是否是和谐函数?
是否是和谐函数?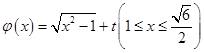 是和谐函数,求实数
是和谐函数,求实数 的取值范围.
的取值范围. 是定义在R上的奇函数,且对任意
是定义在R上的奇函数,且对任意 ,当
,当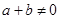 时,都有
时,都有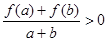 .
.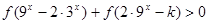 对任意
对任意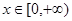 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. 定义域为
定义域为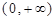 ,且
,且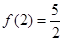 .
. 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点 和
和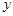 轴的垂线,垂足分别为
轴的垂线,垂足分别为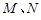 .
.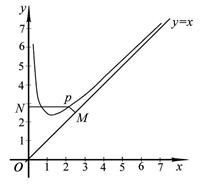
 的单调递减区间(不必证明);(4分)
的单调递减区间(不必证明);(4分) ,求
,求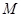 点的坐标(用
点的坐标(用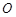 为坐标原点,求四边形
为坐标原点,求四边形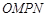 面积的最小值.(7分)
面积的最小值.(7分)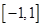 上的偶函数
上的偶函数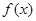 ,已知当
,已知当 时的解析式
时的解析式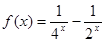
 在
在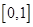 上的解析式;
上的解析式;