题目内容
如图是一个半圆形湖面景点的平面示意图.已知 为直径,且
为直径,且 km,
km, 为圆心,
为圆心, 为圆周上靠近
为圆周上靠近 的一点,
的一点, 为圆周上靠近
为圆周上靠近 的一点,且
的一点,且 ∥
∥ .现在准备从
.现在准备从 经过
经过 到
到 建造一条观光路线,其中
建造一条观光路线,其中 到
到 是圆弧
是圆弧 ,
, 到
到 是线段
是线段 .设
.设 ,观光路线总长为
,观光路线总长为 .
.

(1)求 关于
关于 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
(1) ,
, (2)
(2)
【解析】
试题分析:(1)函数应用题,必须明确题意:观光路线总长为圆弧 与线段
与线段 之和,由弧长公式得
之和,由弧长公式得 ,由直角三角形得
,由直角三角形得 ,所以
,所以 ,根据实际意义得函数的定义域为
,根据实际意义得函数的定义域为
(2)利用导数求函数最值:先求导数 ,再求零点
,再求零点 ,列表分析函数变换趋势得函数
,列表分析函数变换趋势得函数 在
在 处取得极大值,这个极大值就是最大值,即
处取得极大值,这个极大值就是最大值,即 .
.
试题解析:(1)由题意知, , 2分
, 2分
 , 5分
, 5分
因为 为圆周上靠近
为圆周上靠近 的一点,
的一点, 为圆周上靠近
为圆周上靠近 的一点,且
的一点,且 ,
,
所以
所以 ,
, 7分
7分
(2)记 ,则
,则 , 9分
, 9分
令 ,得
,得 , 11分
, 11分
列表
x | (0, |
| ( |
| + | 0 | - |
f (x) | 递增 | 极大值 | 递减 |
所以函数 在
在 处取得极大值,这个极大值就是最大值, 13分
处取得极大值,这个极大值就是最大值, 13分
即 ,
,
答:观光路线总长的最大值为 千米. 14分
千米. 14分
考点:函数解析式,利用导数求函数最值

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 )
)
 ,
, )
)
 不等式
不等式 在
在 上恒成立,则实数
上恒成立,则实数 的取值范围是
的取值范围是 B.
B.  C.
C.  D.
D. 
 ,则“
,则“ ”是“
”是“ ”的
”的 是等差数列,若
是等差数列,若 ,则
,则 的值是 .
的值是 .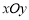 中,已知曲线
中,已知曲线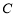 的参数方程是
的参数方程是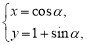 (
(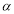 是参数),若以
是参数),若以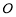 为极点,
为极点,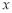 轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线
轴的正半轴为极轴,取与直角坐标系中相同的单位长度,建立极坐标系,求曲线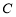 的极坐标方程.
的极坐标方程. ,被直线
,被直线 :
: 反射,反射光线通过点
反射,反射光线通过点 , 则反射光线所在直线的方程是 .
, 则反射光线所在直线的方程是 . 是等差数列,若
是等差数列,若 ,则
,则 的值是 .
的值是 . ,若对于任意
,若对于任意 都有
都有 ,则实数a的取值范围为( )
,则实数a的取值范围为( ) B.
B. C.
C. D.
D.
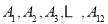 的
的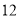 名篮球运动员在某次篮球比赛中的得分记录如下:
名篮球运动员在某次篮球比赛中的得分记录如下:






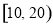 内的运动员中随机抽取
内的运动员中随机抽取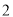 人 , 求这
人 , 求这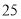 的概率.
的概率.