题目内容
(本小题满分12分)编号分别为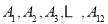 的
的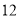 名篮球运动员在某次篮球比赛中的得分记录如下:
名篮球运动员在某次篮球比赛中的得分记录如下:

(1)完成如下的频率分布表:
得分区间 | 频数 | 频率 |
| 3 |
|
| ||
| ||
合计 |
|
|
(2)从得分在区间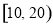 内的运动员中随机抽取
内的运动员中随机抽取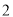 人 , 求这
人 , 求这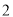 人得分之和大于
人得分之和大于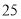 的概率.
的概率.
(1)频率分布表如下:
得分区间 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
合计 |
|
|
(2)这 人得分之和大于
人得分之和大于 的概率为
的概率为 .
.
【解析】
试题分析:(1)根据得分记录进行统计即可完成频率分布表;(2)从得分记录表中可确定得分在区间 内的运动员的编号有5个,从中随机抽取2人,用列举的办法得出所有可能出现的结果数,从中再算出这
内的运动员的编号有5个,从中随机抽取2人,用列举的办法得出所有可能出现的结果数,从中再算出这 人得分之和大于
人得分之和大于 的结果数有多少种,进而根据古典概型的概率计算公式进行计算所求的概率即可.
的结果数有多少种,进而根据古典概型的概率计算公式进行计算所求的概率即可.
试题解析:频率分布表如下
得分区间 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
合计 |
|
|
4分
(2)得分在区间 内的运动员的编号为
内的运动员的编号为 ,
, ,
, ,
, ,
, .从中随机抽取
.从中随机抽取 人,所有可能的抽取结果有:
人,所有可能的抽取结果有: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,共
,共 种.………7分
种.………7分
“从得分在区间 内的运动员中随机抽取
内的运动员中随机抽取 人,这
人,这 人得分之和大于
人得分之和大于 ”(记为事件
”(记为事件 )的所有可能结果有:
)的所有可能结果有: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,共
,共 种10分
种10分
所以 .
.
答:从得分在区间 内的运动员中随机抽取
内的运动员中随机抽取 人,这
人,这 人得分之和大于
人得分之和大于 的概率为
的概率为 …12分.
…12分.
考点: 1.频率分布直方图;2.古典概型.

练习册系列答案
相关题目

















 为直径,且
为直径,且 km,
km, 为圆心,
为圆心, 为圆周上靠近
为圆周上靠近 的一点,
的一点, 为圆周上靠近
为圆周上靠近 的一点,且
的一点,且 ∥
∥ .现在准备从
.现在准备从 经过
经过 到
到 建造一条观光路线,其中
建造一条观光路线,其中 到
到 是圆弧
是圆弧 ,
, .设
.设 ,观光路线总长为
,观光路线总长为 .
.
 关于
关于 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
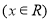 的最小值为a.
的最小值为a.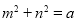 ,求
,求 的最小值.
的最小值.
 C.
C. D.2
D.2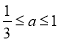 , 若函数
, 若函数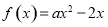 在
在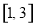 上的最大值为
上的最大值为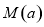 ,最小值为
,最小值为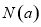 , 令
, 令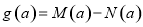 .
.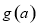 的表达式;
的表达式;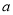 的方程
的方程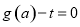 有解,求实数
有解,求实数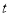 的取值范围.
的取值范围.
 ,
,
 , 其中
, 其中 , 则下列结论中正确的是( )
, 则下列结论中正确的是( ) B.
B. C.
C.  D.
D. 
 的解集是( )
的解集是( ) B.
B. C.
C. D.
D.
 的图象可能是
的图象可能是

 ,B=
,B= ,则
,则 .
.