题目内容
某商品在近100天内,商品的单价f(t)(元)与时间t(天)的函数关系式如下:f(t)=
已知第20天时,该商品的单价为27元,40天时,该商品的单价为32元.
(1)求出实数a,b的值:
(2)已知该种商品的销售量与时间t(天)的函数关系式为g(t)=-
t+
(0≤t≤100,t∈Z).求这种商品在这100天内哪一天的销售额y最高?最高为多少(精确到1元)?
|
(1)求出实数a,b的值:
(2)已知该种商品的销售量与时间t(天)的函数关系式为g(t)=-
| 1 |
| 3 |
| 112 |
| 3 |
分析:(1)根据第20天时,该商品的单价为27元,40天时,该商品的单价为32元,可建立方程组,从而求出实数a,b的值.
(2)先得销售额函数为分段函数,再分段研究函数的最值,从而求出分段函数的最值.
(2)先得销售额函数为分段函数,再分段研究函数的最值,从而求出分段函数的最值.
解答:解:(1)由题意,第20天时,该商品的单价为27元,40天时,该商品的单价为32元.
∴
,
∴
∴a=
,b=22
(2)∵该种商品的销售量与时间t(天)的函数关系式为g(t)=-
t+
(0≤t≤100,t∈Z).
∴销售额为f(t)g(t)=
当0≤t≤40时,y=(
t+22)(-
t+
)=-
(t-12)2+
+12
∴t=12时,ymax=
+12≈833
当40<t≤100时,y=32(-
t+
)是减函数,∴y<32(-
×40+
)<833
综上,当0≤t≤100时,当且仅当t=12时,ymax≈833
答:这种商品在这100天内第12天的销售额最高,最高为833元.
∴
|
∴
|
∴a=
| 1 |
| 4 |
(2)∵该种商品的销售量与时间t(天)的函数关系式为g(t)=-
| 1 |
| 3 |
| 112 |
| 3 |
∴销售额为f(t)g(t)=
|
当0≤t≤40时,y=(
| 1 |
| 4 |
| 1 |
| 3 |
| 112 |
| 3 |
| 1 |
| 12 |
| 112×22 |
| 3 |
∴t=12时,ymax=
| 112×22 |
| 3 |
当40<t≤100时,y=32(-
| 1 |
| 3 |
| 112 |
| 3 |
| 1 |
| 3 |
| 112 |
| 3 |
综上,当0≤t≤100时,当且仅当t=12时,ymax≈833
答:这种商品在这100天内第12天的销售额最高,最高为833元.
点评:本题的考点是函数最值的运用,考查函数模型的构建,考查分段函数的最值问题,解题时应搞清分段函数最值的求解方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
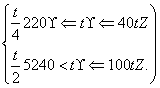
 已知第20天时,该商品的单价为27元,40天时,该商品的单价为32元.
已知第20天时,该商品的单价为27元,40天时,该商品的单价为32元. .求这种商品在这100天内哪一天的销售额y最高?最高为多少(精确到1元)?
.求这种商品在这100天内哪一天的销售额y最高?最高为多少(精确到1元)?