题目内容
2.O是△ABC所在平面上的一点.内角A.B.C所对的边分别是3、4、5,且3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow{0}$.若点P在△ABC的边上.则$\overrightarrow{OA}$•$\overrightarrow{OP}$的取值范围为[-5,10].分析 O为△ABC的内心,建立平面坐标系,分三种情况讨论$\overrightarrow{OA}$•$\overrightarrow{OP}$的取值范围.
解答  解:∵3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow{0}$,∴O是Rt△ABC的内心,
解:∵3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow{0}$,∴O是Rt△ABC的内心,
以CB,CA为x轴,y轴建立平面坐标系,则C(0,0),B(3,0),A(0,4),O(1,1),
∴$\overrightarrow{OA}$=(-1,3),$\overrightarrow{BA}$=(-3,4),$\overrightarrow{OB}$=(2,-1).
(1)若P在线段BC上,设P(x,0),0≤x≤3,则$\overrightarrow{OP}$=(x-1,-1),
∴$\overrightarrow{OA}•\overrightarrow{OP}$=1-x-3=-x-2,
∴-5≤$\overrightarrow{OA}•\overrightarrow{OP}$≤-2,
(2)若P在线段AC上,设P(0,x),0≤x≤4,则$\overrightarrow{OP}$=(-1,x-1),
∴$\overrightarrow{OA}•\overrightarrow{OP}$=1+3(x-1)=3x-2,
∴∴-2≤$\overrightarrow{OA}•\overrightarrow{OP}$≤10.
(3)若P在线段AB上,设$\overrightarrow{BP}$=λ$\overrightarrow{BA}$=(-3λ,4λ),0≤λ≤1,
则$\overrightarrow{OP}$=$\overrightarrow{OB}+\overrightarrow{BP}$=(2-3λ,4λ-1),
∴$\overrightarrow{OA}•\overrightarrow{OP}$=3λ-2+3(4λ-1)=15λ-5,
∴-5≤$\overrightarrow{OA}•\overrightarrow{OP}$≤10.
综上,-5≤$\overrightarrow{OA}•\overrightarrow{OP}$≤10,
故答案为:[-5,10].
点评 本题考查了平面向量的数量积运算,转化为坐标运算是常用方法,属于中档题.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案| A. | ABS(x) | B. | SQR(x) | C. | RND(x) | D. | INT(x) |

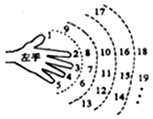 某小朋友按如下规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,7中指,8食指,9大拇指,10食指,…,一直数到2017时,对应的指头是大拇指.
某小朋友按如下规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,7中指,8食指,9大拇指,10食指,…,一直数到2017时,对应的指头是大拇指.