题目内容
1．M是$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1上的动点，已知点F（1，0）、P（3，1），则2|MF|-|MP|的最大值为1．分析 求得椭圆的a，b，c，e和右准线的方程，由椭圆的第二定义可得2|MF|-|MP|的最大值即为d-|MP|的最大值，考虑M，P，K三点共线时，取得最大值．
解答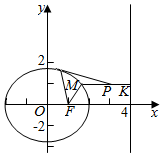 
解：椭圆$\frac{{x}^{2}}{4}$$+\frac{{y}^{2}}{3}$=1的a=2，b=$\sqrt{3}$，c=$\sqrt{{a}^{2}-{b}^{2}}$=1，
e=$\frac{c}{a}$=$\frac{1}{2}$，右准线方程为x=4，
由椭圆的定义可得e=$\frac{|MF|}{d}$=$\frac{1}{2}$，
即有|MF|=$\frac{1}{2}$d（d为M到右准线的距离），
则2|MF|-|MP|的最大值即为d-|MP|的最大值，
当M，P，K三点共线时，d-|MP|取得最大值，且为4-3=1．
故答案为：1．
点评 本题考查椭圆的定义的运用，注意运用转化思想，考查最值的求法，注意运用三点共线的结论，考查运算能力，属于中档题．
练习册系列答案
相关题目
9．已知偶函数f（x）在区间[0，+∞）单调递增，则满足f（2x-1）＜f（$\frac{1}{3}$）的x 取值范围是（ ）
| A． | （$\frac{1}{3}$，$\frac{2}{3}$） | B． | [$\frac{1}{3}$，$\frac{2}{3}$） | C． | （$\frac{1}{2}$，$\frac{2}{3}$） | D． | [$\frac{1}{2}$，$\frac{2}{3}$） |
16．已知平面向量$\overrightarrow{a}$=（x，1），$\overrightarrow{b}$=（2，-3），如果$\overrightarrow a∥\overrightarrow b$，那么x=（ ）
| A． | $\frac{3}{2}$ | B． | -$\frac{3}{2}$ | C． | $\frac{2}{3}$ | D． | -$\frac{2}{3}$ |