题目内容
用五种不同的颜色,给图中的(1)(2)(3)(4)的各部分涂色,每部分涂一种颜色,相邻部分涂不同颜色,则涂色的方法共有 种。

240
【解析】
试题分析:先涂(3)有5种方法,再涂(2)有4种方法,再涂(1)有3种方法,最后涂(4)有4种方法,所以共有5×4×3×4=240种涂色方法。
考点:排列、组合.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
(本题12分) 某县教研室要分析学生初中升学的数学成绩对高一年级数学成绩有什么影响,在高一年级学生中随机抽选10名学生,分析他们入学的数学成绩和高一年级期末数学考试成绩(如下表):
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
入学成绩x | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
高一期末成绩y | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
(1)计算入学成绩 与高一期末成绩
与高一期末成绩 的相关系数;
的相关系数;
(2)对变量 与
与 进行相关性检验,如果
进行相关性检验,如果 与
与 之间具有线性相关关系,求出线性回归方程;(3)若某学生入学数学成绩是80分,试估测他高一期末数学考试成绩。
之间具有线性相关关系,求出线性回归方程;(3)若某学生入学数学成绩是80分,试估测他高一期末数学考试成绩。
分类变量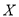 和
和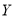 的列联表如下,则( )
的列联表如下,则( )
Y1 | Y2 | 合计 | |
X1 | a | b | a+b |
X2 | c | d | c+d |
合计 | a+c | b+d | a+b+c+d |
A. 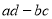 越小,说明
越小,说明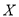 与
与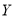 的关系越弱
的关系越弱
B. 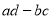 越大,说明
越大,说明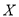 与
与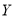 的关系越强
的关系越强
C. 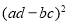 越大,说明
越大,说明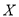 与
与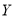 的关系越强
的关系越强
D. 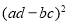 越接近于
越接近于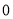 ,说明
,说明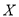 与
与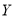 关系越强
关系越强
 表示双曲线,则实数
表示双曲线,则实数 的取值范围是 .
的取值范围是 . ,
, ,则
,则 ( )
( ) B.
B.  C.
C.  D.
D. 
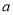 ,
,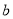 ,
,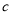 表示空间中三条不同的直线,
表示空间中三条不同的直线, 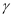 表示平面, 给出下列命题:
表示平面, 给出下列命题: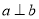 ,
, 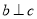 , 则
, 则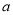 ∥
∥ ; ② 若
; ② 若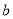 ,
, 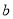 ∥
∥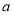 ∥
∥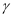 ,
, 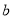 ∥
∥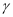 , 则
, 则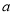 ∥
∥ ; ④ 若
; ④ 若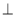
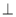

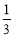
 C.
C.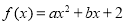 是定义在
是定义在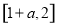 上的偶函数,则
上的偶函数,则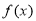 的值域是
的值域是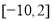 B.
B.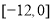
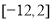 D.与
D.与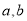 有关,不能确定
有关,不能确定 为等差数列,其前n项和为
为等差数列,其前n项和为 ,已知
,已知 ,
,
 ,若对任意
,若对任意 ,都有
,都有 成立,则k的值为
成立,则k的值为