题目内容
在等差数列{an}中,a2,a16是方程x2-6x-1=0的两根,则a5+a6+a9+a12+a13= .
考点:等差数列的性质
专题:等差数列与等比数列
分析:依题意可得a2+a16=2a9=6,求得a9=3;利用等差数列的性质可得a5+a6+a9+a12+a13=5a9,从而可得答案.
解答:
解:等差数列{an}中,∵a2,a16是方程x2-6x-1=0的两根,
∴a2+a16=2a9=6,
∴a9=3;
由等差数列的性质得:a5+a6+a9+a12+a13=5a9=15;
故答案为:15.
∴a2+a16=2a9=6,
∴a9=3;
由等差数列的性质得:a5+a6+a9+a12+a13=5a9=15;
故答案为:15.
点评:不透考查韦达定理的应用与等差数列的性质,掌握等差中项的性质是解决问题的关键,属于中档题.

练习册系列答案
相关题目
根据如图图案中的圆圈排列规则,猜想第6个图形中的圆圈个数是( )
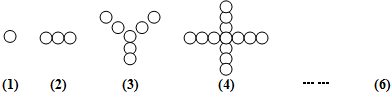

| A、20 | B、25 | C、31 | D、36 |