题目内容
设椭圆E: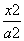 +
+ =1的焦点在x轴上.
=1的焦点在x轴上.
(1)若椭圆E的焦距为1,求椭圆E的方程;
(2)设F1,F2分别是椭圆E的左、右焦点,P为椭圆E上第一象限内的点,直线F2P交y轴于点Q,并且F1P⊥F1Q.证明:当a变化时,点P在某定直线上.
解:(1)因为焦距为1,所以2a2-1=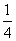 ,解得a2=
,解得a2= .
.
故椭圆E的方程为 =1.
=1.
(2)证明:设P(x0,y0),F1(-c,0),F2(c,0),其中c= .
.
由题设知x0≠c,则直线F1P的斜率kF1P= ,
,
直线F2P的斜率kF2P= .
.
故直线F2P的方程为y= (x-c).
(x-c).
当x=0时,y= ,即点Q坐标为
,即点Q坐标为 .
.
因此,直线F1Q的斜率为kF1Q= .
.
由于F1P⊥F1Q,所以kF1P·kF1Q= =-1.
=-1.
化简得y =x
=x -(2a2-1).①
-(2a2-1).①
将①代入椭圆E的方程,由于点P(x0,y0)在第一象限,解得x0=a2,y0=1-a2,即点P在定直线x+y=1上.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
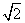 ,求椭圆E的方程.
,求椭圆E的方程.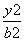 =1(a>b>0)与双曲线
=1(a>b>0)与双曲线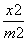 -
-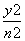 =1(m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是( )
=1(m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是( )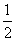 B.
B. D.
D.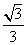
 (B)-
(B)- (D)
(D)
 (D)y=x|x|
(D)y=x|x|