题目内容
已知函数f(x)= ex,a,b
ex,a,b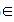 R,且a>0.
R,且a>0.
(1)若a=2,b=1,求函数f(x)的极值;
(2)设g(x)=a(x-1)ex-f(x).
① 当a=1时,对任意x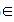 (0,+∞),都有g(x)≥1成立,求b的最大值;
(0,+∞),都有g(x)≥1成立,求b的最大值;
② 设g′(x)为g(x)的导函数.若存在x>1,使g(x)+g′(x)=0成立,求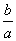 的取值范围.
的取值范围.
 【解析】
【解析】

 所以b≤x2-2x-
所以b≤x2-2x- 在x∈(0,+∞)上恒成立. …………………………………………8分
在x∈(0,+∞)上恒成立. …………………………………………8分
记h(x)=x2-2x- (x>0),则h′(x)=
(x>0),则h′(x)= .
.

 设u(x)=
设u(x)= (x>1),则u′(x)=
(x>1),则u′(x)= .
.
因为x>1,u′(x)>0恒成立,所以u(x)在(1,+∞)是增函数,所以u(x)>u(1)=-1,
所以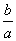 >-1,即
>-1,即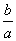 的取值范围为(-1,+∞). …………………………………………16分
的取值范围为(-1,+∞). …………………………………………16分
解法二:因为g (x)=(ax- -2a)ex,所以g ′(x)=(
-2a)ex,所以g ′(x)=( +ax-
+ax- -a)ex.
-a)ex.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 b,sin B=sin C,则B等于________.
b,sin B=sin C,则B等于________. )的值为 .
)的值为 . 
 R,且|x+y|≤
R,且|x+y|≤ ,|x-y|≤
,|x-y|≤ ,求证:|x+5y|≤1.
,求证:|x+5y|≤1. M
M