题目内容
已知函数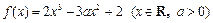 .
.
(Ⅰ)若函数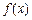 的图象在点
的图象在点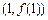 处的切线与直线
处的切线与直线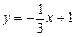 垂直,
垂直,
求函数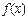 的单调区间;(Ⅱ)求函数
的单调区间;(Ⅱ)求函数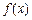 在区间
在区间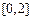 上的最大值.
上的最大值.
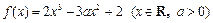 .
.(Ⅰ)若函数
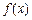 的图象在点
的图象在点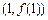 处的切线与直线
处的切线与直线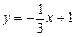 垂直,
垂直,求函数
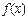 的单调区间;(Ⅱ)求函数
的单调区间;(Ⅱ)求函数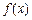 在区间
在区间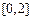 上的最大值.
上的最大值.(Ⅰ)函数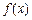 的单调递增区间是
的单调递增区间是 ,
, ;单调递减区间是
;单调递减区间是 .
.
(Ⅱ)
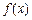 的单调递增区间是
的单调递增区间是 ,
, ;单调递减区间是
;单调递减区间是 .
.(Ⅱ)

:(Ⅰ)∵ ,又
,又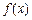 在点
在点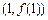 处的切线与直线
处的切线与直线 垂直,
垂直,
∴ ,∴
,∴ .∴
.∴ ,
,
 .由
.由 得
得 或
或 ;由
;由 ,得
,得 .∴函数
.∴函数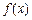 的单调递增区间是
的单调递增区间是 ,
, ;单调递减区间是
;单调递减区间是 .
.
(Ⅱ)∵ ,
, .
.
由 得
得 或
或 ;由
;由 ,得
,得 .∴函数
.∴函数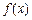 在
在 上递增,在
上递增,在 上递减,在
上递减,在 上递增.
上递增.
∴函数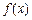 在
在 处取得极大值,
处取得极大值, 处取得极小值.
处取得极小值.
由 ,即
,即 ,解得
,解得 . ①若
. ①若 ,即
,即 时,
时,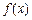 的最大值为
的最大值为 ; ②若
; ②若 ,即
,即 时,
时,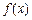 的最大值为
的最大值为 .
.
综上所述,函数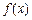 的最大值
的最大值 .
.
 ,又
,又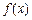 在点
在点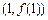 处的切线与直线
处的切线与直线 垂直,
垂直,∴
 ,∴
,∴ .∴
.∴ ,
, .由
.由 得
得 或
或 ;由
;由 ,得
,得 .∴函数
.∴函数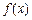 的单调递增区间是
的单调递增区间是 ,
, ;单调递减区间是
;单调递减区间是 .
.(Ⅱ)∵
 ,
, .
.由
 得
得 或
或 ;由
;由 ,得
,得 .∴函数
.∴函数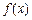 在
在 上递增,在
上递增,在 上递减,在
上递减,在 上递增.
上递增.∴函数
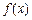 在
在 处取得极大值,
处取得极大值, 处取得极小值.
处取得极小值.由
 ,即
,即 ,解得
,解得 . ①若
. ①若 ,即
,即 时,
时,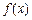 的最大值为
的最大值为 ; ②若
; ②若 ,即
,即 时,
时,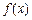 的最大值为
的最大值为 .
. 综上所述,函数
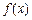 的最大值
的最大值 .
. 
练习册系列答案
相关题目
 数
数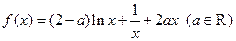
 (1)当
(1)当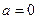 时,求
时,求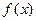 的极值;(2)当
的极值;(2)当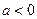 时,求
时,求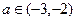 及
及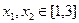 ,恒有
,恒有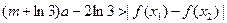 成立,求
成立,求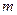 的取值范围
的取值范围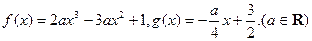
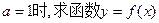 的单调区间;
的单调区间;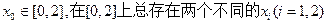 ,使得
,使得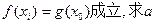 的取值范围.
的取值范围.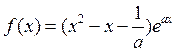 (
(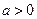 )
)
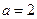 时,求函数
时,求函数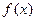 的单调区间;
的单调区间;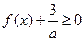 对
对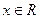 恒成立,求a的取值范围
恒成立,求a的取值范围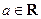 ,函数
,函数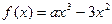 .
.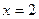 是函数
是函数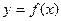 的极值点,求实数
的极值点,求实数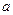 的值;
的值;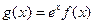 在
在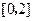 上是单调减函数,求实数
上是单调减函数,求实数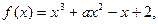
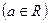
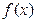 在
在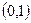 上是减函数,求
上是减函数,求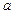 的最大值;
的最大值;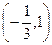 ,求函数y=
,求函数y=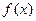 图像过点
图像过点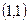 的切线与两坐标轴围成图形的面积。
的切线与两坐标轴围成图形的面积。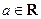 ,函数
,函数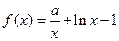 ,
,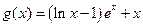 (其中
(其中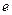 为自然对数的底数).
为自然对数的底数).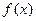 在区间
在区间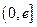 上的最小值;
上的最小值;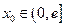 ,使曲线
,使曲线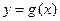 在点
在点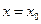 处的切线与
处的切线与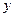 轴垂直? 若存在,求出
轴垂直? 若存在,求出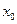 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.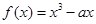 (
(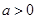 )的零点都在区间[-10,10]上,则使得方程
)的零点都在区间[-10,10]上,则使得方程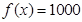 有正整数解的实数
有正整数解的实数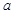 的取值个数为 ( )
的取值个数为 ( )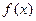 是R上可导的偶函数,
是R上可导的偶函数,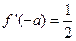 ,则
,则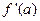 的值为( ).
的值为( ).