题目内容
6.已知一种放射性物质经过120年剩留原来质量的95.76%,设质量为1的这种物质经过x年后剩量为y,则x、y之间的函数关系式为$0.957{6}^{\frac{x}{120}}$.分析 通过设衰变率为p,利用(1-p)120=0.9576计算可得1-p的值,进而代入计算即得结论.
解答 解:设衰变率为p,则(1-p)120=0.9576,
∴1-p=$0.957{6}^{\frac{1}{120}}$,
于是y=(1-p)x=$0.957{6}^{\frac{x}{120}}$,
故答案为:$0.957{6}^{\frac{x}{120}}$.
点评 本题考查函数模型的选择与应用,考查分析问题,解决问题的能力,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
15.若s,t均为正数,且s+t=1,则$\frac{st}{(st+1)(st+4)}$的最大值是( )
| A. | $\frac{4}{85}$ | B. | $\frac{7}{72}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{7}$ |
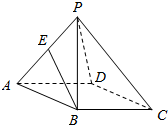 如图,在底面为正方形的四棱锥P-ABCD中,PA=PB=PC=PD=AB=2,点E为棱PA的中点,则异面直线BE与PD所成角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,在底面为正方形的四棱锥P-ABCD中,PA=PB=PC=PD=AB=2,点E为棱PA的中点,则异面直线BE与PD所成角的余弦值为$\frac{\sqrt{3}}{6}$.