题目内容
15.($\frac{1+i}{{\sqrt{2}}}$)2016=1.分析 再利用复数的周期性即可得出.
解答 解:($\frac{1+i}{{\sqrt{2}}}$)2016=$\frac{{{[(1+i)}^{2}]}^{1008}}{{2}^{1008}}$=$\frac{{{2}^{1008}i}^{1008}}{{2}^{1008}}$=i1008=1,
故答案为:1.
点评 本题考查了复数的运算法则、复数的周期性,考查了计算能力,属于基础题.

练习册系列答案
相关题目
6.复数z满足(1+i)z=|$\sqrt{3}$-i|,则$\overline{z}$=( )
| A. | 1+i | B. | 1-i | C. | -1-i | D. | -1+i |
3.在△ABC中,a=3,b=$\sqrt{3}$,A=120°,则B等于( )
| A. | 120° | B. | 60° | C. | 45° | D. | 30° |
 ,且满足
,且满足 ,则
,则 的大小关系是_____________.
的大小关系是_____________.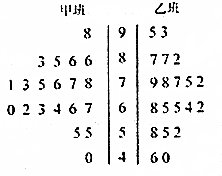 甲、乙两班各20个学生某次数学考试成绩(单位:分)的茎叶图如图所示,根据茎叶图解决下列问题.
甲、乙两班各20个学生某次数学考试成绩(单位:分)的茎叶图如图所示,根据茎叶图解决下列问题.