题目内容
现有一块边长为2的正方形铁皮,其中E为AB的中点,将△ADE与△BEC分别沿ED,EC向上折起,使A、B重合于点P,做成一个垃圾铲,则它的体积为( )
A、
| ||||
B、
| ||||
| C、1 | ||||
| D、2 |
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:这个四面体可以看成是以E点为顶点,以△ADC为底面的三棱锥,只要求出底面三角形面积,以及高的长度,再代入三棱锥的体积公式即可.
解答:
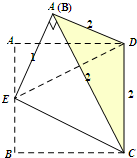 解:∵△ADC的三边分别为AB,AC,BC,∴AB=2,AC=2,BC=2
解:∵△ADC的三边分别为AB,AC,BC,∴AB=2,AC=2,BC=2
∴S△ADC=
×2×2×
=
∵在正方形中,EA⊥AD,EB⊥BC,四面体中,EA、EB重合,
∴四面体中,EA⊥AD,EA⊥BC,∴EA⊥平面ADC
∴三棱锥E-ADC的高为EA,又∵EA=1
∴VE-ADC=
×
×1=
.
故选:A.
 解:∵△ADC的三边分别为AB,AC,BC,∴AB=2,AC=2,BC=2
解:∵△ADC的三边分别为AB,AC,BC,∴AB=2,AC=2,BC=2∴S△ADC=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∵在正方形中,EA⊥AD,EB⊥BC,四面体中,EA、EB重合,
∴四面体中,EA⊥AD,EA⊥BC,∴EA⊥平面ADC
∴三棱锥E-ADC的高为EA,又∵EA=1
∴VE-ADC=
| 1 |
| 3 |
| 3 |
| ||
| 3 |
故选:A.
点评:本题考查了三棱锥体积公式的运用,其中涉及到折叠问题,一定要抓住折叠后的不变量.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,三个几何体,一个是长方体、一个是直三棱柱,一个是过圆柱上下底面圆心切下圆柱的四分之一部分,这三个几何体的主视图和俯视图是相同的长方形,则它们的体积之比为( )
如图,三个几何体,一个是长方体、一个是直三棱柱,一个是过圆柱上下底面圆心切下圆柱的四分之一部分,这三个几何体的主视图和俯视图是相同的长方形,则它们的体积之比为( )| A、4:2:π | ||
B、4:2:
| ||
| C、4:1:π | ||
| D、2:1:π |
已知复数z满足条件:(1+2i)z=1,则z对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
用二分法求函数f(x)=2x-3的零点时,初始区间可选为( )
| A、(-1,0) |
| B、(0,1) |
| C、(2,3) |
| D、(1,2) |
(文)设三角形ABC的三个内角为A,B,C,向量
=(
sinA,sinB),
=(cosB,
cosA),
•
=1+cos(A+B),则C=( )
| m |
| 3 |
| n |
| 3 |
| m |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
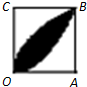 在正方形OABC框格内有一块花纹(如图所示),花纹刚好过点O,B,经研究发现花纹边界是函数y=x2与
在正方形OABC框格内有一块花纹(如图所示),花纹刚好过点O,B,经研究发现花纹边界是函数y=x2与