题目内容
若双曲线
-
=1的两个焦点为F1、F2，|F1F2|=10，P为双曲线上的一点，|PF1|=2|PF2|，PF1⊥PF2，求此双曲线的方程．
| x2 |
| a2 |
| y2 |
| b2 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据双曲线的定义，及勾股定理，可确定几何量之间的关系，求出几何量，即可求出双曲线的方程．
解答：
解：设|PF2|=m，则|PF1|=2m
∴|PF1|-|PF2|=2a=m
∴m=2a
∵PF1⊥PF2，|
∴16a2+4a2=4c2=100
∴a2=5
∴b2=25-5=20，
∴双曲线的方程为
-
=1．
∴|PF1|-|PF2|=2a=m
∴m=2a
∵PF1⊥PF2，|
∴16a2+4a2=4c2=100
∴a2=5
∴b2=25-5=20，
∴双曲线的方程为
| x2 |
| 5 |
| y2 |
| 20 |
点评：本题考查双曲线的定义，考查双曲线的几何性质，解题的关键是确定几何量之间的关系．
练习册系列答案
相关题目
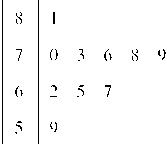已知某单位有50名职工，现要从中抽取10名职工，将全体职工随机按1～50编号，并按编号顺序平均分成10组进行系统抽样．