题目内容
14.正三角形ABC的边长为1,点P、Q由点C出发,分别沿线段CA、CB前进,CP与时间t(0<t≤1)的关系是|CP|=t2,CQ与时间t的关系是$|CQ|=\sqrt{t}$,记y为三角形CPQ的面积,则y的大致图象是( )| A. | 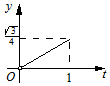 | B. | 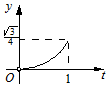 | C. | 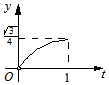 | D. | 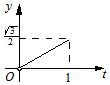 |
分析 求出函数的解析式,利用幂函数的图象,可得结论.
解答 解:0<t≤1,|CP|=t2,CQ与时间t的关系是$|CQ|=\sqrt{t}$,
∴y=$\frac{1}{2}{t}^{2}\sqrt{t}sin60°$=$\frac{\sqrt{3}}{4}{t}^{\frac{5}{2}}$,图象的形状是开口向上的抛物线,
故选B.
点评 本题考查函数的解析式与图象,考查幂函数图象,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.某学校对手工社、摄影社两个社团招新报名的情况进行调查,得到如下的2×2列联表:
(1)请填上上表中所空缺的五个数字;
(2)能否在犯错误的概率不超过0.05的前提下,认为学生对这两个社团的选择与“性别”有关系?
(注:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d)
| 手工社 | 摄影社 | 总计 | |
| 女生 | 6 | ||
| 男生 | 42 | ||
| 总计 | 30 | 60 |
(2)能否在犯错误的概率不超过0.05的前提下,认为学生对这两个社团的选择与“性别”有关系?
(注:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d)
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
9.对任意的实数R,集合A={x|x2+x-6>0},B={-1,0,1,2,3,4}.则B∩∁RA=( )
| A. | {2,3,4,5} | B. | {-1,0} | C. | {-1,0,1,2} | D. | { 2,3,4} |