题目内容
 如图,多面体ABC-A1B1C1中,三角形ABC是边长为4的正三角形,AA1∥BB1∥CC1,AA1⊥平面ABC,AA1=BB1=2CC1=4.
如图,多面体ABC-A1B1C1中,三角形ABC是边长为4的正三角形,AA1∥BB1∥CC1,AA1⊥平面ABC,AA1=BB1=2CC1=4.(1)若O是AB的中点,求证:OC1⊥A1B;
(2)在线段AB1上是否存在一点D,使得CD∥平面A1B1C1,若存在确定D的位置;若不存在,说明理由.
考点:直线与平面平行的性质,空间中直线与直线之间的位置关系
专题:综合题,空间位置关系与距离
分析:(1)取线段A1B1的中点为E,连接OE,C1E,CO,证明AB⊥面EOCC1,利用A1B1∥AB,OC?面EOCC1,可得OC1⊥A1B;
(2)设OE∩AB1=D,则点D是AB1的中点,证明四边形CC1ED是平行四边形即可.
(2)设OE∩AB1=D,则点D是AB1的中点,证明四边形CC1ED是平行四边形即可.
解答:
 (1)证明:取线段A1B1的中点为E,连接OE,C1E,CO
(1)证明:取线段A1B1的中点为E,连接OE,C1E,CO
已知等边ABC是边长为4,AA1=BB1=2CC1=4,AA1⊥平面ABC,AA1∥BB1∥
CC1,
∴AA1B1B是正方形,
∴OE⊥AB,CO∥AB,
又∵CO∩OE=O,
∴AB⊥面EOCC1,
∵A1B1∥AB,OC?面EOCC1,
∴OC1⊥A1B…(6分)
(2)解:设OE∩AB1=D,则点D是AB1的中点,
∴ED∥AA1,ED=
AA1…(8分)
又∵CC1∥AA1,CC1=
AA1,
∴四边形CC1ED是平行四边形,…(10分)
∴CD∥C1E,∴CD∥平面A1B1C1,
即存在点D使得CD∥平面A1B1C1,点D是AB1的中点.…(12分)
 (1)证明:取线段A1B1的中点为E,连接OE,C1E,CO
(1)证明:取线段A1B1的中点为E,连接OE,C1E,CO已知等边ABC是边长为4,AA1=BB1=2CC1=4,AA1⊥平面ABC,AA1∥BB1∥
CC1,
∴AA1B1B是正方形,
∴OE⊥AB,CO∥AB,
又∵CO∩OE=O,
∴AB⊥面EOCC1,
∵A1B1∥AB,OC?面EOCC1,
∴OC1⊥A1B…(6分)
(2)解:设OE∩AB1=D,则点D是AB1的中点,
∴ED∥AA1,ED=
| 1 |
| 2 |
又∵CC1∥AA1,CC1=
| 1 |
| 2 |
∴四边形CC1ED是平行四边形,…(10分)
∴CD∥C1E,∴CD∥平面A1B1C1,
即存在点D使得CD∥平面A1B1C1,点D是AB1的中点.…(12分)
点评:本题考查线面平行的判定,考查线面垂直,正确运用判定定理是关键.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、有两个面互相平行,其余各面都是平行四边形的几何体是棱柱 |
| B、用一个平面去截一个圆锥,只能得到一个圆锥和一个圆台 |
| C、有一个面是多边形,其余面都是三角形的几何体是棱锥 |
| D、将一个直角三角形绕其一条直角边旋转一周,所得圆锥母线长等于斜边长 |
下列几何体中不是旋转体的是( )
A、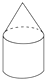 |
B、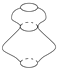 |
C、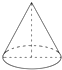 |
D、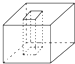 |
下表为某大型超市一个月的销售收入情况表,则本月销售收入的平均增长率( )
| 日期 | 5 | 10 | 15 | 20 | 25 | 30 |
| 销售收入(万元) | 20 | 40 | 90 | 160 | 275 | 437.5 |
| A、一样 | B、越来越大 |
| C、越来越小 | D、无法确定 |