题目内容
16.y=$\frac{1}{tanx}$(x∈[-$\frac{π}{4}$,$\frac{π}{4}$]且x≠0)的值域是[1,+∞)∪(-∞,-1].分析 根据正切函数的图象与性质,求出x∈[-,]时函数y=tanx的值域即可.
解答 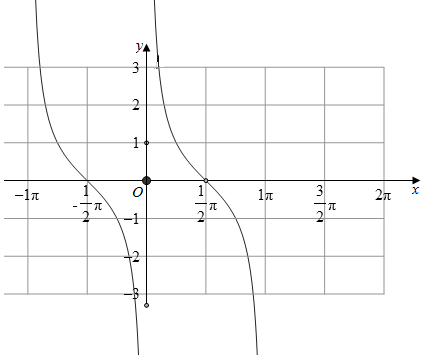 解;∵y=$\frac{1}{tanx}$(x∈[-$\frac{π}{4}$,$\frac{π}{4}$]且x≠0)
解;∵y=$\frac{1}{tanx}$(x∈[-$\frac{π}{4}$,$\frac{π}{4}$]且x≠0)
∴根据y=tanx单调性
画出图象得出:[-$\frac{π}{4}$,0)(0,$\frac{π}{4}$]都是单调递减函数.
x=$\frac{π}{4}$,y=1,x=-$\frac{π}{4}$,y=-1,
∴x→+0,y→+∞,x→-0,y→-∞,
函数值域:y=$\frac{1}{tanx}$的值域为[1,+∞)∪(-∞,-1].
故答案:[1,+∞)∪(-∞,-1].
点评 本题考查了正切函数的图象与性质的应用问题,是基础题目.

练习册系列答案
相关题目
6.某学校共有3125名学生,一次活动中全体学生被排成一个n排的等腰梯形阵,且这n排学生数按每排都比前一排
多一人的规律排列,则当n取到最大值时,排在这等腰梯形阵最外面的一周的学生总人数是( )
多一人的规律排列,则当n取到最大值时,排在这等腰梯形阵最外面的一周的学生总人数是( )
| A. | 296 | B. | 221 | C. | 225 | D. | 641 |
7.已知函数f(x)=2sin2(ωx+$\frac{π}{6}$)(ω>0)在区间[$\frac{π}{6}$,$\frac{2π}{3}$]内单调递增,则ω的最大值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
8.已知不等式9ax+8≥$\frac{36x}{2{x}^{2}+1}$+1在[$\frac{1}{2}$,+∞)上恒成立,则实数a的取值范围是( )
| A. | ($\frac{8}{9}$,+∞) | B. | (-∞,$\frac{8}{9}$) | C. | [$\frac{8}{9}$,+∞) | D. | (-∞,$\frac{8}{9}$] |