题目内容
已知f(x)是R上的奇函数,且当x∈(0,+∞)时f(x)=x(1+
),则当x∈(-∞,0)时,f(x)等于( )
| 3 | x |
A、-x(1+
| |||
B、x(1+
| |||
C、-x(1-
| |||
D、x(1-
|
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:由f(x)是R上的奇函数,由x∈(-∞,0)时,-x∈(0,+∞),故f(-x)可代入已知解析式求解,再由奇函数可求出f(x).
解答:
解:当x∈(-∞,0)时,-x∈(0,+∞),
∵当x∈(0,+∞)时f(x)=x(1+
),
∴f(-x)=-x(1+
)=-x(1-
),
又∵f(x)是奇函数,
∴f(x)=-f(-x)=x(1-
),
故选:D
∵当x∈(0,+∞)时f(x)=x(1+
| 3 | x |
∴f(-x)=-x(1+
| 3 | -x |
| 3 | x |
又∵f(x)是奇函数,
∴f(x)=-f(-x)=x(1-
| 3 | x |
故选:D
点评:本题考查函数的奇偶性的应用、求函数的解析式.考查计算能力.

练习册系列答案
相关题目
已知α是第四象限角,且sinα=-
,则tan2α的值为( )
| 4 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
曲线
(θ为参数)的对称中心( )
|
| A、在直线y=2x上 |
| B、在直线y=-2x上 |
| C、在直线y=x-3上 |
| D、在直线y=x+3上 |
过点(0,4)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有( )
| A、1条 | B、2条 | C、3条 | D、4条 |
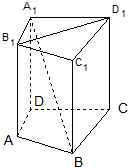 如图,在直四棱柱A1B1C1 D1-ABCD中,当底面四边形ABCD满足条件
如图,在直四棱柱A1B1C1 D1-ABCD中,当底面四边形ABCD满足条件