题目内容
已知数列{an}满足a1=
,
=
,求数列{an}的通项公式.
| 1 |
| 2 |
| 1 |
| 2an+1 |
| 1 |
| 2an+1 |
考点:数列递推式
专题:等差数列与等比数列
分析:由数列递推式得到2an+1=2an+1,进一步得到an+1-an=
.则数列{an}是以
为公差的等差数列,然后直接代入等差数列的通项公式得答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:由
=
,得2an+1=2an+1,
即an+1=an+
,∴an+1-an=
.
则数列{an}是以
为公差的等差数列.
又a1=
,
∴an=a1+
(n-1)=
+
-
=
.
| 1 |
| 2an+1 |
| 1 |
| 2an+1 |
即an+1=an+
| 1 |
| 2 |
| 1 |
| 2 |
则数列{an}是以
| 1 |
| 2 |
又a1=
| 1 |
| 2 |
∴an=a1+
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
点评:本题考查了数列递推式,考查了等差关系的确定,考查了等差数列的通项公式,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
,把函数g(x)=f(x)-
x的偶数零点按从小到大的顺序排列成一个数列,该数列的前n项的和Sn,则S2015=( )
|
| 1 |
| 2 |
| A、1007×2015 |
| B、1008×2015 |
| C、2014×2015 |
| D、2015×2016 |
在△ABC中,角A,B,C的对边分别是a,b,c,且A,B,C成等差数列,a+c=2,则b的取值范围是( )
| A、[1,2) | ||
| B、(0,2] | ||
C、[1,
| ||
| D、[1,+∞) |
如果tan(α+β)=
,tan(α-
)=
,那么tan(β+
)=( )
| 3 |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|

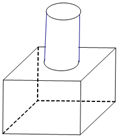 某机器零件是如图所示的几何体(实心),零件下面是边长为10cm的正方体,上面是底面直径为4cm,高为10cm的圆柱.
某机器零件是如图所示的几何体(实心),零件下面是边长为10cm的正方体,上面是底面直径为4cm,高为10cm的圆柱.