Question

函数f(x)=2^x,x₁,x₂∈R且x₁＜x₂，若a=(x₁+x₂)，则恒成立的是

A.|f(a)-f(x₁)|＞|f(x₂)-f(a)|                        B.|f(a)-f(x₁)|＜|f(x₂)-f(a)|

C.f(x₁)f(x₂)＞［f(a)］²                          D.|f(a)-f(x₁)|=|f(x₂)-f(a)|

Answer 1

B  函数f(x)=2^x在R上为增函数,由x₁＜x₂,a=(x₁+x₂),

∴|f(a)-f(x₁)|=f(a)-f(x₁),|f(x₂)-f(a)|=f(x₂)-f(a),=

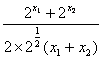
=［(x₁-x₂)+(x₂-x₁)］＞×2=1.

∵f(x)＞0,∴f(x₁)+f(x₂)＞2f(a).∴f(a)-f(x₁)＜f(x₂)-f(a),即|f(a)-f(x₁)|＜|f(x₂)-f(a)|.