题目内容
在△ABC中,化简cos4A+cos4B+cos4C-4cos2Acos2Bcos2C=
-3
-3
.分析:先cos4A用二倍角公式化成2A的关系,再由2A=2π-2B-2C运用两角和与差的公式进行化简合并.
解答:解:∵cos4A+cos4B+cos4C-4cos2Acos2Bcos2C
=2cos22A-1+2cos22B-1+2cos22C-1-4cos2Acos2Bcos2C
=2cos2(2π-2B-2C)+2cos22B+2cos22C-4cos(2π-2B-2C)cos2Bcos2C-3
=2cos2(2B+2C)+2cos22B+2cos22C-4cos(2B+2C)cos2Bcos2C-3
=2(cos22Bcos22C+sin22Bsin22C-2cos2Bcos2Csin2Bsin2C)+2cos22B+2cos22C-4(cos2Bcos2C-sin2Bsin2C)cos2Bcos2C-3
=2cos22Bcos22C+2sin22Bsin22C-4cos2Bcos2Csin2Bsin2C+2cos22B+2cos22C-4cos22Bcos22C-4sin2Bsin2Ccos2Bcos2C-3
=2sin22Bsin22C+2cos22B+2cos22C-2cos22Bcos22C-3
=2cos22B(1-cos22C)+2sin22Bsin22C+2cos22C-3
=sin22C(2sin22B+2cos22B)+2cos22C-3
=2sin22C)+2cos22C-3
=-3
故答案为:-3.
=2cos22A-1+2cos22B-1+2cos22C-1-4cos2Acos2Bcos2C
=2cos2(2π-2B-2C)+2cos22B+2cos22C-4cos(2π-2B-2C)cos2Bcos2C-3
=2cos2(2B+2C)+2cos22B+2cos22C-4cos(2B+2C)cos2Bcos2C-3
=2(cos22Bcos22C+sin22Bsin22C-2cos2Bcos2Csin2Bsin2C)+2cos22B+2cos22C-4(cos2Bcos2C-sin2Bsin2C)cos2Bcos2C-3
=2cos22Bcos22C+2sin22Bsin22C-4cos2Bcos2Csin2Bsin2C+2cos22B+2cos22C-4cos22Bcos22C-4sin2Bsin2Ccos2Bcos2C-3
=2sin22Bsin22C+2cos22B+2cos22C-2cos22Bcos22C-3
=2cos22B(1-cos22C)+2sin22Bsin22C+2cos22C-3
=sin22C(2sin22B+2cos22B)+2cos22C-3
=2sin22C)+2cos22C-3
=-3
故答案为:-3.
点评:本题主要考查二倍角公式和两角和与差的余弦公式.这里注意是在三角形中解题,故内角和为π是经常被用到的.

练习册系列答案
相关题目
 向量
向量 ,
,
 的解析式,并求函数的单调递减区间;
的解析式,并求函数的单调递减区间; 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知 的面积为
的面积为 ,求
,求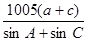 .
.