题目内容
△ABC中，a=
，b=1，B=30°，则A等于（ ）
| 3 |
| A、60° |
| B、60°或120° |
| C、30°或150° |
| D、30° |
考点：正弦定理
专题：解三角形
分析：直接用正弦定理求得sinA的值，进而求得A．
解答：
解：∵
=
，
∴sinA=
=
=
．
∵0°＜A＜180°，
∴B=60°或120°，
故选：B．
| a |
| sinA |
| b |
| sinB |
∴sinA=
| asinB |
| b |
| ||||
| 1 |
| ||
| 2 |
∵0°＜A＜180°，
∴B=60°或120°，
故选：B．
点评：本题主要考查了正弦定理的应用．用正弦定理的条件一般时知三求一．
练习册系列答案
相关题目
“x2-4x+3＞0”是“x＜1或x＞4”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设集合A={2，3，5，8}，B={3，5，7，9}，则集合A∩B=（ ）
| A、{2，3，5，7，8} |
| B、{5} |
| C、{3，5} |
| D、{2，8，7，9} |
在下列函数中，最小值是2的是（ ）
A、y=
| ||||
B、y=
| ||||
C、y=sinx+
| ||||
| D、y=7x+7-x |
在△ABC中，已知A=75°，B=60°，c=2，则b等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a、b、c满足a＞b＞c，且a+b+c=0，那么下列选项中不一定成立的是（ ）
| A、ab＞ac |
| B、c（b-a）＜0 |
| C、cb2＜ab2 |
| D、ac（a-c）＜0 |
如图程序运行后输出的结果为（ ）
| A、22；-22 |
| B、-22；22 |
| C、6；-6 |
| D、-6；6 |
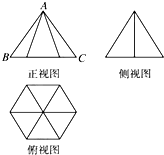一个几何体的三视图如图所示，其中正视图中△ABC是边长为2的正三角形，俯视图为正六边形，求该几何体的侧视图的面积．