题目内容
已知函数f(x)=2|sinx|+3sinx,x∈[-π,π]
(1)求函数f(x)的值域;
(2)设函数g(x)=f(x)-k;
①讨论函数g(x)的零点个数;
②若存在x∈[-
,
],使不等式g(x)≥k2+5成立,求k的取值范围.
(1)求函数f(x)的值域;
(2)设函数g(x)=f(x)-k;
①讨论函数g(x)的零点个数;
②若存在x∈[-
| π |
| 4 |
| 5π |
| 6 |
考点:三角函数中的恒等变换应用,分段函数的应用
专题:三角函数的图像与性质
分析:(1)根据sinx的符号化简解析式,再由正弦函数的性质求出函数f(x)的值域;
(2)①根据(1)化简的解析式、正弦函数的图象作出f(x)的大致图象,由图得直线y=k与y=f(x)的图象交点个数以及对应k的取值范围;
②根据图象和x的范围求出f(x)的值域,再求出g(x)的最大值,将不等式恒成立问题转化为g(x)max≥k2+5,解关于k得不等式即可.
(2)①根据(1)化简的解析式、正弦函数的图象作出f(x)的大致图象,由图得直线y=k与y=f(x)的图象交点个数以及对应k的取值范围;
②根据图象和x的范围求出f(x)的值域,再求出g(x)的最大值,将不等式恒成立问题转化为g(x)max≥k2+5,解关于k得不等式即可.
解答:
解:(1)由题意得,f(x)=2|sinx|+3sinx=
----------(3分)
当-π≤-x≤0时,f(x)∈[-1,0];当0<x≤π时,f(x)∈(0,5],
所以f(x)的值域为f(x)∈[-1,5];----------------------(6分)
(2)①由(1)得,f(x)=
,作出f(x)的大致图象如图所示:----(8分)
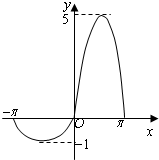 函数g(x)=f(x)-k零点个数,即方程f(x)-k=0或f(x)=k的实根个数,
函数g(x)=f(x)-k零点个数,即方程f(x)-k=0或f(x)=k的实根个数,
也即直线y=k与y=f(x)的图象交点个数,
由图象可知,当k<-1或k>5时,函数没有零点;
当k=-1或k=5时,函数有一个零点;
当-1<k<0或0<k<5时,函数有两个零点;
当k=0时,函数有三个零点.--------(12分)
②由x∈[-
,
]和图象得,f(x)∈[-
,5],
故g(x)max=5-k,
因为存在x∈[-
,
],使不等式g(x)≥k2+5成立,
只需g(x)max=5-k≥k2+5,即k(k+1)≤0,
所以k的取值范围是[-1,0]------(16分)
|
当-π≤-x≤0时,f(x)∈[-1,0];当0<x≤π时,f(x)∈(0,5],
所以f(x)的值域为f(x)∈[-1,5];----------------------(6分)
(2)①由(1)得,f(x)=
|
 函数g(x)=f(x)-k零点个数,即方程f(x)-k=0或f(x)=k的实根个数,
函数g(x)=f(x)-k零点个数,即方程f(x)-k=0或f(x)=k的实根个数,也即直线y=k与y=f(x)的图象交点个数,
由图象可知,当k<-1或k>5时,函数没有零点;
当k=-1或k=5时,函数有一个零点;
当-1<k<0或0<k<5时,函数有两个零点;
当k=0时,函数有三个零点.--------(12分)
②由x∈[-
| π |
| 4 |
| 5π |
| 6 |
| ||
| 2 |
故g(x)max=5-k,
因为存在x∈[-
| π |
| 4 |
| π |
| 3 |
只需g(x)max=5-k≥k2+5,即k(k+1)≤0,
所以k的取值范围是[-1,0]------(16分)
点评:本题考查正弦函数的图象和性质的应用,分段函数值域,函数零点的转化,恒成立转化为求函数的最值问题,以及数形结合思想和转化思想.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
方程x3+3x-3=0的解在区间( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
若实数x、y满足
且z=2x+y的最小值为3,则实数b=( )
|
A、
| ||
B、
| ||
| C、3 | ||
| D、5 |
在棱长为1的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM与CN所成角的余弦值是( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,过圆O外一点P分别作圆的切线PA和割线PB,且PB=9,C是圆上一点使得BC=4,∠BAC=∠APB,则AB=
如图,过圆O外一点P分别作圆的切线PA和割线PB,且PB=9,C是圆上一点使得BC=4,∠BAC=∠APB,则AB= 如图所示,在正方体ABCD-A1B1C1D1中:
如图所示,在正方体ABCD-A1B1C1D1中: