题目内容
设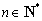 ,函数
,函数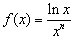 ,函数
,函数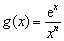 ,
,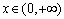 .
.
(Ⅰ)当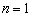 时,写出函数
时,写出函数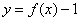 零点个数,并说明理由;
零点个数,并说明理由;
(Ⅱ)若曲线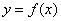 与曲线
与曲线 分别位于直线
分别位于直线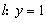 的两侧,求
的两侧,求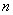 的所有可能取值.
的所有可能取值.
解析:(Ⅰ)证明:结论:函数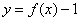 不存在零点.
不存在零点.
当 时,
时, ,求导得
,求导得 ,
,
令 ,解得
,解得 .
.
当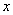 变化时,
变化时, 与
与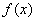 的变化如下表所示:
的变化如下表所示:
|
|
|
|
|
|
|
| 0 |
|
|
| ↗ | ↘ |
所以函数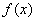 在
在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
则当 时,函数
时,函数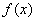 有最大值
有最大值 .
.
所以函数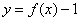 的最大值为
的最大值为 ,
,
所以函数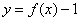 不存在零点.
不存在零点.
(Ⅱ)解:由函数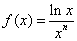 求导,得
求导,得  ,
,
令 ,解得
,解得 .
.
当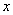 变化时,
变化时, 与
与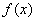 的变化如下表所示:
的变化如下表所示:
|
|
|
|
|
|
|
| 0 |
|
|
| ↗ | ↘ |
所以函数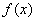 在
在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
则当 时,函数
时,函数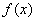 有最大值
有最大值 ;
;
由函数 ,
, 求导,得
求导,得  ,
,
令  ,解得
,解得 .
.
当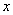 变化时,
变化时,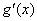 与
与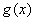 的变化如下表所示:
的变化如下表所示:
|
|
|
|
|
|
|
| 0 |
|
|
| ↘ | ↗ |
所以函数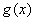 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
则当 时,函数
时,函数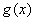 有最小值
有最小值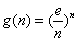 .
.
因为 ,函数
,函数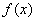 有最大值
有最大值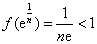 ,
,
所以曲线 在直线
在直线 的下方,而曲线
的下方,而曲线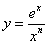 在直线
在直线 的上方,
的上方,
所以 ,解得
,解得 .
.
所以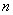 的取值集合为
的取值集合为 .
.

某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如右数据:
| 单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量 | 90 | 84 | 83 | 80 | 75 | 68 |
由表中数据,求得线性回归方程为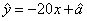 .若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
.若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.








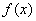 =
= .
.  的解集;
的解集; 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数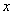 的取值范围.
的取值范围. 的值是( )
的值是( )
 (B)
(B) (C)
(C) (D)
(D)
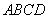 的周长为
的周长为 ,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为 .
,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为 .
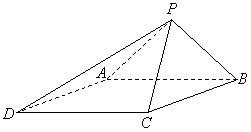
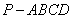 的底面为菱形,
的底面为菱形,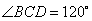 ,
,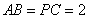 ,
,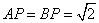 .
.

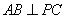 ;
;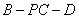 的余弦值.
的余弦值. 中,
中, ,
, ,
, ,将其沿对角线
,将其沿对角线 折成四面体
折成四面体 ,使平面
,使平面
 平面
平面 ,若四面体
,若四面体 (B)
(B) (C)
(C) (D)
(D)
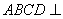 平面
平面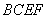 ,且四边形
,且四边形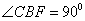 ,
,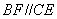 ,
,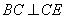 ,
,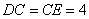 ,
,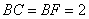 .
.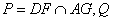 是直线
是直线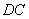 上的动点,判断并证明直线
上的动点,判断并证明直线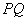 与直线
与直线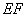 的位置关系.
的位置关系.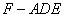 的体积.
的体积.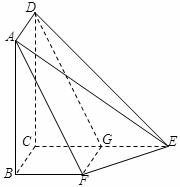
 (元)
(元) (件)
(件) 的一条渐近线为
的一条渐近线为 ,则它的离心率为
,则它的离心率为 B.
B. C.
C. D.
D.