题目内容
已知函数f(x)=alnx+1(a>0)
(Ⅰ)若a=2,求函数f(x)在(e,f(e))处的切线方程;
(Ⅱ)当x>0时,求证:f(x)-1≥a(1-
).
(Ⅰ)若a=2,求函数f(x)在(e,f(e))处的切线方程;
(Ⅱ)当x>0时,求证:f(x)-1≥a(1-
| 1 |
| x |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)把a=2代入函数解析式,求导后求得f′(e)的值,再求出f(e)的值,由直线方程的点斜式求得切线方程;
(Ⅱ)构造辅助函数g(x)=f(x)-1-a(1-
),利用导数求得该函数的最小值,由最小值大于等于0证得答案.
(Ⅱ)构造辅助函数g(x)=f(x)-1-a(1-
| 1 |
| x |
解答:
(Ⅰ)解:当a=2时,f(x)=2lnx+1,
f′(x)=
,f(e)=3,k=f′(e)=
.
∴函数f(x)在(e,f(e))处的切线方程为y-3=
(x-e),
即2x-ey+e=0;
(Ⅱ)证明:令g(x)=f(x)-1-a(1-
)=alnx-a(1-
)(x>0),
则g′(x)=
-
=
,由g′(x)=0,得x=1.
当0<x<1时,g′(x)<0,g(x)在(0,1)上单调递减,
当x>1时,g′(x)>0,g(x)在(1,+∞)上单调递增.
∴g(x)在x=1处取得极小值,也是最小值,
因此g(x)≥g(1)=0,即f(x)-1≥a(1-
).
f′(x)=
| 2 |
| x |
| 2 |
| e |
∴函数f(x)在(e,f(e))处的切线方程为y-3=
| 2 |
| e |
即2x-ey+e=0;
(Ⅱ)证明:令g(x)=f(x)-1-a(1-
| 1 |
| x |
| 1 |
| x |
则g′(x)=
| a |
| x |
| a |
| x2 |
| a(x-1) |
| x2 |
当0<x<1时,g′(x)<0,g(x)在(0,1)上单调递减,
当x>1时,g′(x)>0,g(x)在(1,+∞)上单调递增.
∴g(x)在x=1处取得极小值,也是最小值,
因此g(x)≥g(1)=0,即f(x)-1≥a(1-
| 1 |
| x |
点评:本题考查利用导数研究曲线的切线方程,考查了利用导数研究函数的最值,训练了函数构造法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
执行如图所示的程序框图,则输出S的值为( )
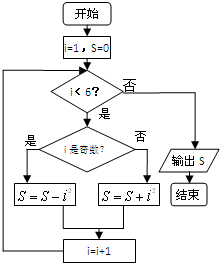

| A、3 | B、-6 | C、10 | D、-15 |
 如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.
如图,已知动圆M过定点F(0,1)且与x轴相切,点F关于圆心M的对称点为F′,动点F′的轨迹为C.