题目内容
已知a、b∈R,ab≠0则在(1)
≥ab,(2)
+
≥2,(3)ab≤(
)2,(4)(
)2≤
这四个不等式中,恒成立的是 (填序号)
| a2+b2 |
| 2 |
| b |
| a |
| a |
| b |
| a+b |
| 2 |
| a+b |
| 2 |
| a2+b2 |
| 2 |
考点:不等式的基本性质
专题:不等式的解法及应用
分析:(1)由(a-b)2≥0,展开即可得出;
(2)ab<0,不成立;
(3)由a2+b2≥2ab,可得(a+b)2≥4ab,即可得出;
(4)由a2+b2≥2ab,可得2(a2+b2)≥(a+b)2,即可得出.
(2)ab<0,不成立;
(3)由a2+b2≥2ab,可得(a+b)2≥4ab,即可得出;
(4)由a2+b2≥2ab,可得2(a2+b2)≥(a+b)2,即可得出.
解答:
解:(1)∵(a-b)2≥0,∴
≥ab;
(2)ab<0,
+
≥2不成立;
(3)∵a2+b2≥2ab,∴(a+b)2≥4ab,∴ab≤(
)2,正确;
(4)∵a2+b2≥2ab,∴2(a2+b2)≥(a+b)2,∴(
)2≤
,正确.
综上可得:只有(1)(3)(4)正确.
故答案为:(1)(3)(4).
| a2+b2 |
| 2 |
(2)ab<0,
| b |
| a |
| a |
| b |
(3)∵a2+b2≥2ab,∴(a+b)2≥4ab,∴ab≤(
| a+b |
| 2 |
(4)∵a2+b2≥2ab,∴2(a2+b2)≥(a+b)2,∴(
| a+b |
| 2 |
| a2+b2 |
| 2 |
综上可得:只有(1)(3)(4)正确.
故答案为:(1)(3)(4).
点评:本题考查了重要不等式与基本不等式的性质,考查了推理能力与变形能力,属于基础题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
已知数列{an}的前n项和Sn=n2-4n,第m项满足5<an<8,则m=( )
| A、9 | B、8 | C、7 | D、6 |
已知函数f(
)=
(x≠0,x≠1),且那么f(x)的解析式为( )
| 1 |
| x |
| 1 |
| x+1 |
A、
| ||
B、
| ||
C、
| ||
| D、1+x |
 在三棱锥P-ABC中,O为AC中点,PA=PB=PC=AC=2,AB=BC=
在三棱锥P-ABC中,O为AC中点,PA=PB=PC=AC=2,AB=BC=




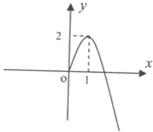 已知奇函数f(x)在[0,+∞)上的图象是如图所示的抛物线的一部分.
已知奇函数f(x)在[0,+∞)上的图象是如图所示的抛物线的一部分.