题目内容
2.已知定义在R上的可导函数f(x)的导函数为f'(x),满足f'(x)<f(x),且f(x+2)=f(-x+2),f(4)=1,则不等式f(x)<ex的解集为( )| A. | (-∞,e4) | B. | (e4,+∞) | C. | (-∞,0) | D. | (0,+∞) |
分析 构造函数g(x)=$\frac{f(x)}{{e}^{x}}$,利用导数和已知即可得出其单调性.再利用函数的奇偶性和已知可得g(0)=1,即可得出.
解答 解:构造函数g(x)=$\frac{f(x)}{{e}^{x}}$,则g′(x)=$\frac{{f}^{′}(x)-f(x)}{{e}^{x}}$<0,∴函数g(x)在R上单调递减,
∴函数f(-x+2)=f(x+2),
∴函数关于x=2对称,
∴f(0)=f(4)=1,
原不等式等价为g(x)<1,
∵g(0)=$\frac{f(0)}{{e}^{0}}$=1.
∴g(x)<1?g(x)<g(0),
∵g(x)在R上单调递减,
∴x>0.
∴不等式f(x)<ex的解集为(0,+∞).
故选:D.
点评 本题考查了利用导数研究函数的单调性、利用函数的单调性解不等式、函数的奇偶性及对称性,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
14.复数$\frac{3-i}{1-i}$在复平面上所对应的点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
10.设三条不同的直线l1,l2,l3满足l1⊥l3,l2⊥l3,则l1与l2( )
| A. | 是异面直线 | B. | 是相交直线 | ||
| C. | 是平行直线 | D. | 可能相交,或相交,或异面直线 |
17.在某化学反应的中间阶段,压力保持不变,温度从1℃变化到5℃,反应结果如表所示(x表示温度,y代表结果):
(1)求化学反应的结果y对温度x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(2)判断变量x与y之间是正相关还是负相关,并预测当温度到达10℃时反应结果为多少?
附:线性回归方程中$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$.
| x | 1 | 2 | 3 | 4 | 5 |
| y | 3 | 5 | 7 | 10 | 11 |
(2)判断变量x与y之间是正相关还是负相关,并预测当温度到达10℃时反应结果为多少?
附:线性回归方程中$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$.
7.要得到函数$y=\frac{{\sqrt{2}}}{2}sinx+\frac{{\sqrt{2}}}{2}cosx+1$的图象,需要把函数y=sinx的图象( )
| A. | 向右平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| B. | 向左平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| C. | 向左平移$\frac{π}{4}$个单位,再向下平移1个单位 | |
| D. | 向右平移$\frac{π}{4}$个单位,再向下平移1个单位 |
12.函数f(x)=x2-2x+3的值域是( )
| A. | (-∞,2] | B. | (0,+∞) | C. | [2,+∞) | D. | [0,2] |
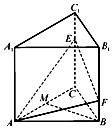 三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2.
三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2.