题目内容
7.已知函数f(x)=$\frac{3x}{x+1}$,x∈[2,5].(1)判断f(x)的单调性并且证明;
(2)求f(x)在区间[2,5]上的最大值和最小值.
分析 (1)直接利用函数的单调性的定义证明即可.
(2)利用函数的单调性,直接求解函数的最值即可.
解答 解:(1)f(x)在[2,5]上是增函数.
理由:在[2,5]上任取两个数x1<x2,
则有$f({x_1})-f({x_2})=\frac{{3{x_1}}}{{{x_1}+1}}-\frac{{3{x_2}}}{{{x_2}+1}}$=$\frac{{3({x_1}-{x_2})}}{{({x_1}+1)({x_2}+1)}}$<0,
所以f(x)在[2,5]上是增函数.
(2)由(1)可知函数是增函数,
f(x)在区间[2,5]上的最大值f(2)=2;最小值f(5)=$\frac{5}{2}$.
点评 本题考查函数的单调性以及函数的最值的求法,考查计算能力.

练习册系列答案
相关题目
12.设a=2-3,b=log35,c=cos100°,则( )
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>b>a |
17.已知P(-1,2),过P点且与原点距离最大的直线的方程是( )
| A. | x+2y-5=0 | B. | 2x-y+5=0 | C. | x-2y+5=0 | D. | 2x+y-5=0 |
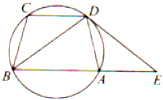 如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.
如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.