题目内容
19.平面内有点A(2,0),C(cosα,sinα),其中α∈(0,π),点O为坐标原点,且|$\overrightarrow{OA}$+$\overrightarrow{OC}$|=$\sqrt{7}$.(1)求α的值;
(2)求向量$\overrightarrow{OA}$与$\overrightarrow{AC}$的夹角.
分析 (1)由已知求出$\overrightarrow{OA}$+$\overrightarrow{OC}$的坐标,再由|$\overrightarrow{OA}$+$\overrightarrow{OC}$|=$\sqrt{7}$求得cosα,进一步得到α的值;
(2)由(1)求得C的坐标,得到$\overrightarrow{AC}$的坐标,求出$\overrightarrow{OA}$•$\overrightarrow{AC}$及|$\overrightarrow{OA}$|与|$\overrightarrow{AC}$|,代入数量积求夹角公式可得向量$\overrightarrow{OA}$与$\overrightarrow{AC}$的夹角.
解答 解:(1)由题意$\overrightarrow{OA}$+$\overrightarrow{OC}$=(2+cosα,sinα),
则|$\overrightarrow{OA}$+$\overrightarrow{OC}$|=$\sqrt{(2+cosα)^{2}+si{n}^{2}α}=\sqrt{7}$,
解得:cos$α=\frac{1}{2}$.
又α∈(0,π),∴$α=\frac{π}{3}$;
(2)由(1)知,C($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),∴$\overrightarrow{AC}=(-\frac{3}{2},\frac{\sqrt{3}}{2})$,则$|\overrightarrow{AC}|=\sqrt{3}$.
∴cos<$\overrightarrow{OA},\overrightarrow{AC}$>=$\frac{\overrightarrow{OA}•\overrightarrow{AC}}{|\overrightarrow{OA}||\overrightarrow{AC}|}$=$\frac{-3}{2×\sqrt{3}}=-\frac{\sqrt{3}}{2}$.
又<$\overrightarrow{OA},\overrightarrow{AC}$>∈(0,π),
∴向量$\overrightarrow{OA}$与$\overrightarrow{AC}$的夹角为$\frac{5π}{6}$.
点评 本题考查平面向量的数量积运算,考查由数量积求夹角公式,是中档题.

| A. | c<a<b | B. | a<c<b | C. | c<b<a | D. | b<c<a |
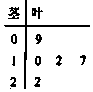 如图是一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的平均数、中位数分别为( )
如图是一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的平均数、中位数分别为( )| A. | 14,12 | B. | 12,14 | C. | 14,10 | D. | 10,12 |
| A. | $\frac{3}{8}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{2}$ |