题目内容
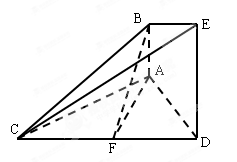
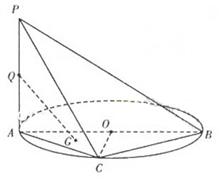
如图的几何体中,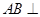 平面
平面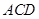 ,
,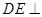 平面
平面 ,△
,△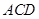 为等边三角形,
为等边三角形,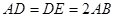 ,
,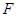 为
为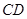 的中点.
的中点.
(1)求证: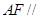 平面
平面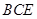 ;
;
(2)求证:平面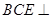 平面
平面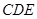 .
.
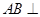 平面
平面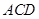 ,
,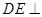 平面
平面 ,△
,△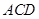 为等边三角形,
为等边三角形,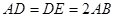 ,
,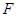 为
为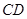 的中点.
的中点.
(1)求证:
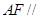 平面
平面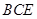 ;
;(2)求证:平面
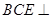 平面
平面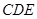 .
.证明见解析.
试题分析:(1)要证线面平行,关键是在平面内找一条与待证直线平行的直线,本题中,由于
 ,
,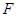 是中点,故很容易让人联想到取另一中点,这里我们取
是中点,故很容易让人联想到取另一中点,这里我们取 中点
中点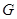 ,则
,则 ∥
∥ ∥
∥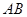 ,
, ,故
,故 是平行四边形,从而有
是平行四边形,从而有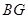 ∥
∥ ,平行线找到了,结论得证;(2)要证面垂直,就是要证线面垂直,关键是找哪个平面内的直线,同样本题里由于
,平行线找到了,结论得证;(2)要证面垂直,就是要证线面垂直,关键是找哪个平面内的直线,同样本题里由于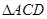 是等边三角形,故
是等边三角形,故 ,从而很快得到结论
,从而很快得到结论 平面
平面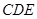 ,而(1)中有
,而(1)中有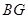 ∥
∥ ,则有
,则有 平面
平面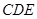 ,这就是我们要的平面的垂线,由此就证得了面面垂直.
,这就是我们要的平面的垂线,由此就证得了面面垂直.试题解析:(1)证明:取
 的中点
的中点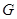 ,连结
,连结 .
.∵
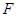 为
为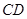 的中点,∴
的中点,∴ 且
且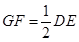 .
.∵
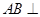 平面
平面 ,
,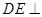 平面
平面 ,
, ∴
 ,∴
,∴ . 又
. 又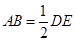 ,∴
,∴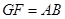 .
. ∴四边形
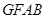 为平行四边形,则
为平行四边形,则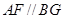 .
. ∵
 平面
平面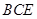 ,
,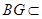 平面
平面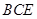 , ∴
, ∴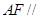 平面
平面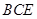 . 7分
. 7分(2)证明:∵
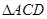 为等边三角形,
为等边三角形,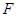 为
为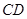 的中点,∴
的中点,∴
∵
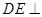 平面
平面 ,
,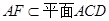 ,∴
,∴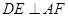 .
. ∵
 ,∴
,∴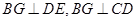 又
又 ,
, ∴
 平面
平面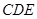 .
.∵
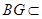 平面
平面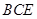 , ∴平面
, ∴平面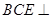 平面
平面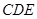 . 14分
. 14分

练习册系列答案
相关题目
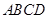 中,
中,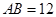 ,
,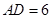 ,
,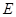 、
、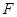 分别为
分别为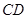 、
、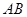 边上的点,且
边上的点,且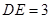 ,
,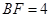 ,将
,将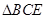 沿
沿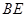 折起至
折起至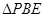 位置(如图2所示),连结
位置(如图2所示),连结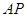 、
、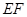 、
、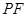 ,其中
,其中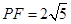 .
.
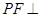 平面
平面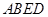 ;
;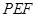 所成角的正弦值.
所成角的正弦值.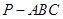 中,
中,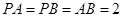 ,
,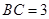 ,
,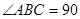 °,平面
°,平面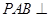 平面
平面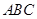 ,
,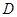 、
、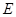 分别为
分别为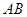 、
、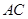 中点.
中点.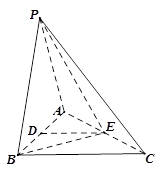
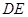 ∥平面
∥平面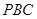 ;
;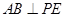 ;
; 的大小.
的大小.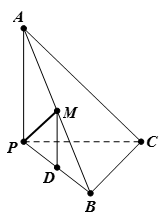
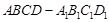 中,已知
中,已知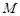 是棱
是棱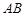 的中点.
的中点.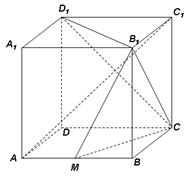
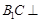 平面
平面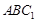 ,
,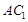 ∥平面
∥平面 ;
;


 平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.
平面ABCD,且AD= 2PA,E、F、G、H分别是线段PA、PD、CD、BC的中点.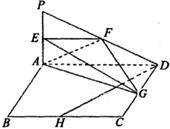
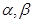 是两个不同的平面,
是两个不同的平面, 是一条直线,则下列命题正确的是( )
是一条直线,则下列命题正确的是( )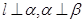 ,则
,则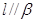
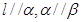 ,则
,则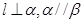 ,则
,则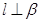
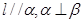 ,则
,则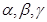 是三个不同的平面,上述命题中真命题的是
是三个不同的平面,上述命题中真命题的是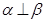 ,
,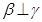 ,则
,则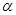 ∥
∥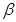 ;
;