题目内容
12.已知函数f(x)=ln$\frac{ex}{e-x}$,若f($\frac{e}{2016}$)+f($\frac{2e}{2016}$)+…+f($\frac{2015e}{2016}$)=$\frac{2015}{4}$(a+b),则a2+b2的最小值为8.分析 由已知得f(x)+f(e-x)=ln$\frac{ex}{e-x}$+ln$\frac{e(e-x)}{e-(e-x)}$=lne2=2,由此利用均值定理能求出a2+b2的最小值.
解答 解:∵f(x)=ln$\frac{ex}{e-x}$,
∴f(x)+f(e-x)=ln$\frac{ex}{e-x}$+ln$\frac{e(e-x)}{e-(e-x)}$=lne2=2,
∴$\frac{2015}{4}$(a+b)=f($\frac{e}{2016}$)+f($\frac{2e}{2016}$)+…+f($\frac{2015e}{2016}$)=$\frac{1}{2}×(2×2015)$=2015,
∴a+b=4,
∴${a}^{2}+{b}^{2}≥\frac{(a+b)^{2}}{2}$=8,当且仅当a=b=2时取等号,
∴a2+b2的最小值为8.
故答案为:8.
点评 本题考查代数式的和的最小值的求法,是基础题,解题时要认真审题,注意函数性质和均值定理的合理运用.

练习册系列答案
相关题目
3.已知函数f(x)是R上的减函数,且f(-1)=4,f(2)=-2.设P={x|f(x+t)≤4},Q={x|f(x)≤-2}.若“x∈P”是“x∈Q”的充分不必要条件,则实数t的取值范围是( )
| A. | t≤-3 | B. | t<-3 | C. | t≥-3 | D. | t>-3 |
4.已知m>0,两圆x2+y2=m与x2+(y-m)2=20相交于A,B两点,且在点A处两圆的切线互相垂直,则线段AB的长度为( )
| A. | 3 | B. | 3$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
12.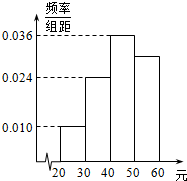 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元.
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元.
 学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元.
学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出在[20,60)元的样本,其频率分布直方图如图所示,根据此图估计学生在课外读物方面的支出费用的中位数为( )元.| A. | 45 | B. | 46 | C. | $\frac{390}{9}$ | D. | $\frac{400}{9}$ |