题目内容
13.函数f(x)=$\frac{x}{lnx}$的单调递减区间是( )| A. | (0,e) | B. | (0,1),(1,e) | C. | (e,+∞) | D. | (-∞,e) |
分析 求出导函数,结合函数的定义域判断函数的单调减区间即可.
解答 解:f(x)=$\frac{x}{lnx}$,
∴f'(x)=$\frac{lnx-1}{(lnx)^{2}}$,
∴当x∈(0,1)和(1,e)时,f'(x)<0,f(x)递减.
故选B.
点评 考查了利用导函数求函数的单调区间,易错点是注意函数的定义域.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.设a,b,c大于0,则3个数$\frac{a}{b},\frac{b}{c},\frac{c}{a}$的值( )
| A. | 至多有一个不大于1 | B. | 都大于1 | ||
| C. | 至少有一个不大于1 | D. | 都小于1 |
3.已知直线l1:3x+4y=0和l2:3x-4y=0的倾斜角( )
| A. | 互补 | B. | 互余 | C. | 相等 | D. | 互为相反数 |
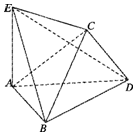 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.