题目内容
10.已知抛物线的参数方程为$\left\{{\begin{array}{l}{x=4{t^2}}\\{y=4t}\end{array}}\right.$,若斜率为1的直线经过抛物线的焦点,且与抛物线相交于A,B两点,则线段AB的长为( )| A. | $2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | 8 | D. | 4 |
分析 先根据抛物线方程求得抛物线的焦点坐标,进而根据点斜式求得直线的方程与抛物线方程联立,消去y,根据韦达定理求得x1+x2=的值,进而根据抛物线的定义可知|AB|=x1+$\frac{p}{2}$+x2+$\frac{p}{2}$,求得答案.
解答 解:抛物线的参数方程为$\left\{{\begin{array}{l}{x=4{t^2}}\\{y=4t}\end{array}}\right.$,普通方程为y2=4x,抛物线焦点为(1,0),且斜率为1,
则直线方程为y=x-1,代入抛物线方程y2=4x得
x2-6x+1=0,设A(x1,y1),B(x2,y2)
∴x1+x2=6
根据抛物线的定义可知|AB|=x1+$\frac{p}{2}$+x2+$\frac{p}{2}$
=x1+x2+p=6+2=8,
故选C.
点评 本题主要考查了直线与圆锥曲线的关系,抛物线的简单性质.对学生基础知识的综合考查.关键是:将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系,利用弦长公式即可求得|AB|值,从而解决问题.

练习册系列答案
相关题目
20.在△ABC中,角A,B,C所对的边分别为a,b,c,且a,2b,c成等比数列,则cosB的最小值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{8}$ |
1.已知集合M={x∈R|x2+2x=0},N={2,0},则M∩N=( )
| A. | {0} | B. | {2} | C. | ∅ | D. | {-2,0,2} |
19.“a3>b3”是“a>b”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 ,则△ABC的外心一定在满足条件的P点集合中;
,则△ABC的外心一定在满足条件的P点集合中;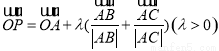 ,则△ABC的内心一定在满足条件的P点集合中;
,则△ABC的内心一定在满足条件的P点集合中;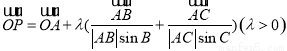 ,则△ABC的重心一定在满足条件的P点集合中;
,则△ABC的重心一定在满足条件的P点集合中;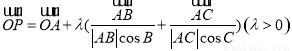 ,则△ABC的垂心一定在满足条件的P点集合中.
,则△ABC的垂心一定在满足条件的P点集合中.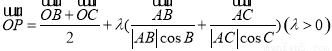 ,则△ABC的外心一定在满足条件的P点集合中.
,则△ABC的外心一定在满足条件的P点集合中.