题目内容
已知a是实数,则函数f(x)=x2(x-a)在[0,2]上的最大值是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:由条件利用二次函数的性质,分类讨论求得函数f(x)在[0,2]上的最大值.
解答:
解:函数f(x)=x2(x-a)的图象的对称轴方程为x=
,
当
<1,即a<2时,函数f(x)=x2(x-a)在[0,2]上的最大值是f(2)=8-4a;
当
≥1,即a≥2时,函数f(x)=x2(x-a)在[0,2]上的最大值是f(0)=0,
故答案为:
.
| a |
| 2 |
当
| a |
| 2 |
当
| a |
| 2 |
故答案为:
|
点评:本题主要考查二次函数的性质,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
抛物线y2=8x的焦点到双曲线x2-
=1的一条渐近线的距离为( )
| y2 |
| 3 |
| A、1 | ||
| B、2 | ||
C、
| ||
D、2
|
在平面直角坐标系xOy中,双曲线的中心在原点,焦点在y轴上,一条渐近线方程为x-2y=0,则它的离心率为( )
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线
-
=1(a>0,b>0)的一条渐近线的斜率为
,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
若P={y|y=|x|},Q={x|-
≤x≤
},则P∩Q=( )
| 2 |
| 2 |
A、(0,
| ||||
| B、{(1,1),(-1,-1)} | ||||
C、[0,
| ||||
D、(-
|
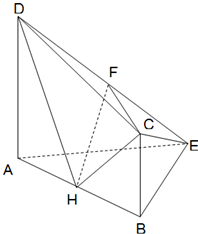 如图,平面ABCD⊥平面ABE,四边形ABCD是直角梯形,AD∥BC,AD⊥AB,BC=
如图,平面ABCD⊥平面ABE,四边形ABCD是直角梯形,AD∥BC,AD⊥AB,BC=