题目内容
19.已知△ABC中,BC=$\sqrt{3}$,AC=2,角A=60°,则边AB=( )| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}+\frac{1}{2}$ |
分析 由已知利用余弦定理可得AB2-2AB+1=0,即可解得AB的值.
解答 解:∵BC=$\sqrt{3}$,AC=2,角A=60°,
∴由余弦定理BC2=AB2+AC2-2AB•AC•cosA,
可得:3=AB2+4-2AB,即:AB2-2AB+1=0,
解得:AB=1.
故选:C.
点评 本题主要考查了余弦定理在解三角形中的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列命题中:
①若x2-3x+2=0,则x=1或x=2
②若-2≤x≤3,则(x+2)(x-3)≤0
③若x=y=0,则x2+y2=0
④若x、y∈N*,x+y是奇数,则x、y中一个是奇数,一个是偶数.
那么( )
①若x2-3x+2=0,则x=1或x=2
②若-2≤x≤3,则(x+2)(x-3)≤0
③若x=y=0,则x2+y2=0
④若x、y∈N*,x+y是奇数,则x、y中一个是奇数,一个是偶数.
那么( )
| A. | ①的逆命题为真 | B. | ②的否命题为假 | C. | ③的逆否命题为假 | D. | ④的逆命题为假 |
11.函数f(x)=x3-3x2在区间[-2,4]上的最大值为( )
| A. | -4 | B. | 0 | C. | 16 | D. | 20 |
9.已知条件p:|x+1|>2,条件q:x>a,且¬p是¬q的充分不必要条件,则a的取值范围是( )
| A. | a≤-3 | B. | a≤1 | C. | a≥-1 | D. | a≥1 |
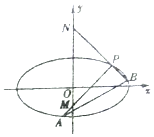 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆的四个顶点为顶点的四边形的面积为8.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,以椭圆的四个顶点为顶点的四边形的面积为8.