题目内容
11.已知定点F1(-2,0)与F2(2,0),动点M满足|MF1|-|MF2|=4,则点M的轨迹方程是( )| A. | $\frac{x^2}{16}-\frac{y^2}{12}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{12}=0(x≥2)$ | C. | y=0(|x|≥2) | D. | y=0(x≥2) |
分析 设出M的坐标,利用两点间的距离公式和题设等式建立方程,平方后化简整理求得y=0,同时|MF1|>|MF2|,可推断出 动点M的轨迹,是一条射线,起点是(2,0),方向同x轴正方向.
解答 解:假设M(x,y),根据|MF1|-|MF2|=2,可以得到:$\sqrt{(x+1)^{2}+{y}^{2}}$-$\sqrt{(x-1)^{2}+{y}^{2}}$=2,
两边平方,化简可以得到y=0,又因为|F1F2|=2,且|MF1|>|MF2|,
所以:动点M的轨迹,是一条射线,起点是(2,0),方向同x轴正方向.
故选D
点评 本题主要考查了轨迹方程.考查了学生分析问题和解决问题的能力.

练习册系列答案
相关题目
1.抛物线y2=ax的准线方程是x=2,则a的值是( )
| A. | 8 | B. | $\frac{1}{8}$ | C. | -8 | D. | $-\frac{1}{8}$ |
2.已知数列{an}是递增等差数列,且a1+a4=8,a2a3=15,设${b_n}=\frac{1}{{{a_n}•{a_{n+1}}}}$,则数列{bn}的前10项和为( )
| A. | $\frac{9}{19}$ | B. | $\frac{18}{19}$ | C. | $\frac{20}{21}$ | D. | $\frac{10}{21}$ |
20.执行图中程序框图,若输入x1=2,x2=3,x3=7,则输出的T值为( )
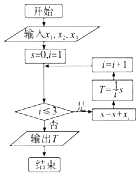

| A. | 3 | B. | 4 | C. | $\frac{11}{3}$ | D. | 5 |
1.下列函数中,既不是奇函数又不是偶函数的是( )
| A. | y=x2+|x| | B. | y=2x-2-x | C. | y=x2-3x | D. | y=$\frac{1}{x+1}$+$\frac{1}{x-1}$ |