题目内容
已知点A(0,2),椭圆C:
+
=1(a>b>0)的右焦点为F,直线AF的斜率为-
,以焦点F和短轴两端点为顶点的三角形周长为6,O为坐标原点.
(1)求椭圆C的方程
(2)设过点A的定直线l与C交于P,Q两点,当△OPQ的面积为1时,求定直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
(1)求椭圆C的方程
(2)设过点A的定直线l与C交于P,Q两点,当△OPQ的面积为1时,求定直线l的方程.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)运用斜率公式,求出c,再由周长为6,得到a+b=3,再由a,b,c的关系式,解方程,即可得到a,b,进而得到椭圆方程;
(2)设直线l:y=kx+2,联立椭圆方程,消去y,得到x的方程,运用韦达定理和判别式大于0,以及弦长公式和点到直线的距离公式,再由三角形的面积公式,列出方程,解出k,即可得到直线方程.
(2)设直线l:y=kx+2,联立椭圆方程,消去y,得到x的方程,运用韦达定理和判别式大于0,以及弦长公式和点到直线的距离公式,再由三角形的面积公式,列出方程,解出k,即可得到直线方程.
解答:
解:(1)设右焦点为F(c,0),由于直线AF的斜率为-
,
即有
=-
,解得,c=
,则a2-b2=c2=3,
又以焦点F和短轴两端点为顶点的三角形周长为6,
则2a+2b=6,即有a+b=3,则a+b=1,解得a=2,b=1.
则椭圆C的方程为
+y2=1;
(2)设直线l:y=kx+2,联立椭圆方程,消去y,得到
(1+4k2)x2+16kx+12=0,
则有△>0,即(16k)2-48(1+4k2)>0,①
x1+x2=-
,x1x2=
,
弦长|PQ|=
•
=
•
=
•
,
O到直线l的距离为d=
,
则有△OPQ的面积为
d•|PQ|=
=1,
解得,k2=
,即有k=±
,代入①,检验成立.
故直线l的方程为:y=±
x+2.
2
| ||
| 3 |
即有
| 2 |
| -c |
2
| ||
| 3 |
| 3 |
又以焦点F和短轴两端点为顶点的三角形周长为6,
则2a+2b=6,即有a+b=3,则a+b=1,解得a=2,b=1.
则椭圆C的方程为
| x2 |
| 4 |
(2)设直线l:y=kx+2,联立椭圆方程,消去y,得到
(1+4k2)x2+16kx+12=0,
则有△>0,即(16k)2-48(1+4k2)>0,①
x1+x2=-
| 16k |
| 1+4k2 |
| 12 |
| 1+4k2 |
弦长|PQ|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
(
|
=
| 1+k2 |
| ||
| 1+4k2 |
O到直线l的距离为d=
| 2 | ||
|
则有△OPQ的面积为
| 1 |
| 2 |
| ||
| 1+4k2 |
解得,k2=
| 7 |
| 4 |
| ||
| 2 |
故直线l的方程为:y=±
| ||
| 2 |
点评:本题考查椭圆的方程和性质,考查联立直线方程和椭圆方程,消去未知数,运用韦达定理和弦长公式,以及点到直线的距离公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
380°角是第几象限角( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
命题“?x∈R,x≥sinx”的否定是( )
| A、?x∈R,x<sinx |
| B、?x∈R,x≤sinx |
| C、?x∈R,x<sinx |
| D、?x∈R,x<sinx |
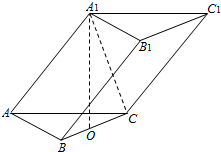 在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=
在三棱柱ABC-A1B1C1中,已知AB=AC=AA1=