题目内容
设函数f(x)在区间(a,b)的导函数为f′(x),f′(x)在区间(a,b)的导函数记为f″(x),若在区间(a,b)上的f″(x)<0恒成立,则称函数f(x)在区间(a,b)上为“凸函数”.已知函数f(x)=
x4-
mx3-4x2+2,且当实数m满足|m|<3时,函数f(x)在区间(a-b,a+b)为“凸函数”,则a2+(b-3)2的最小值为( )
| 1 |
| 6 |
| 1 |
| 3 |
| A、2 | B、4 | C、6 | D、8 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:根据“凸函数”的定义,求出对应的求解,利用线性规划的应用即可得到结论.
解答:
 解:∵f(x)=
解:∵f(x)=
x4-
mx3-4x2+2,
∴f′(x)=4×
x3-mx2-8x,
f″(x)=2x2-2mx-8,
当|m|<3时,f″(x)=2x2-2mx-8<0恒成立,
即x2-mx-4<0恒成立,
?当-3<m<3时,g(m)=-xm+x2-4<0恒成立,
即
,
,
即
,解得-1<x<1.
则(a-b,a+b)⊆(-1,1),
即
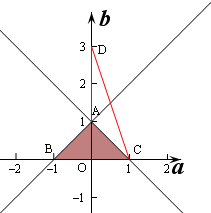
,作出不等式组对应的平面区域如图:
a2+(b-3)2的几何意义是动点P(a,b)到定点D(0,3)的距离的平方,由图象可知,当P位于A(0,1)时,
a2+(b-3)2的最小值为02+(1-3)2=4,
故选:B.
 解:∵f(x)=
解:∵f(x)=| 1 |
| 6 |
| 1 |
| 3 |
∴f′(x)=4×
| 1 |
| 6 |
f″(x)=2x2-2mx-8,
当|m|<3时,f″(x)=2x2-2mx-8<0恒成立,
即x2-mx-4<0恒成立,
?当-3<m<3时,g(m)=-xm+x2-4<0恒成立,
即
|
|
即
|
则(a-b,a+b)⊆(-1,1),
即
|
a2+(b-3)2的几何意义是动点P(a,b)到定点D(0,3)的距离的平方,由图象可知,当P位于A(0,1)时,
a2+(b-3)2的最小值为02+(1-3)2=4,
故选:B.
点评:本题主要考查新定义的应用,利用导数结合二次函数,线性规划以及距离公式是解决本题的关键.综合性较强,难度较大.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
对于定义域为D的函数y=f(x)和常数c,若对任意正实数ξ,?x∈D,使得0<|f(x)-c|<ξ恒成立,则称函数y=f(x)为“敛c函数”,现给出如下函数:
①f(x)=x(x∈Z);
②f(x)=(
)x+2(x∈Z);
③f(x)=log2x+1;
④f(x)=
.
其中为“敛2函数”的有( )
①f(x)=x(x∈Z);
②f(x)=(
| 1 |
| 2 |
③f(x)=log2x+1;
④f(x)=
| 2x-1 |
| 2x |
其中为“敛2函数”的有( )
| A、①② | B、③④ |
| C、①②③ | D、②③④ |
复数z=i(1-2i),(其中i为虚数单位)的实部为( )
| A、-1 | B、1 | C、-2 | D、2 |
已知i是虚数单位,则复数-i(1+i)的实部与虚部的和等于( )
| A、2 | B、0 | C、-2 | D、1-i |