题目内容
在△ABC中,内角A,B,C的对边分别为a,b,c.已知b(cosA-2cosC)=(2c-a)cosB.
(Ⅰ)求
的值;
(Ⅱ)若cosB=
,△ABC的周长为5,求b.
(Ⅰ)求
| c |
| a |
(Ⅱ)若cosB=
| 1 |
| 4 |
考点:余弦定理,三角函数中的恒等变换应用,正弦定理
专题:三角函数的求值
分析:(Ⅰ)已知等式利用正弦定理化简,整理后利用两角和与差的正弦函数公式及诱导公式化简,再利用正弦定理化简即可求出所求式子的值;
(Ⅱ)由第一问c=2a,代入a+b+c=5中,表示出b,利用余弦定理列出关系式,将表示出的b,c以及cosB代入求出a的值,即可确定出b的值.
(Ⅱ)由第一问c=2a,代入a+b+c=5中,表示出b,利用余弦定理列出关系式,将表示出的b,c以及cosB代入求出a的值,即可确定出b的值.
解答:
解:(Ⅰ)在△ABC中,有
=
=
=2R,
又b(cosA-2cosC)=(2c-a)cosB,
∴sinB(cosA-2cosC)=(2sinC-sinA)cosB,即sinBcosA-2sinBcosC=2sinCcosB-sinAcosB,
∴sin(A+B)=2sin(B+C),即sinC=2sinA,
则c=2a,即
=2;
(Ⅱ)由(Ⅰ)∵c=2a,a+b+c=5,
∴b=5-(a+c)=5-3a,
由余弦定理得:b2=c2+a2-2accosB,
∴(5-3a)2=(2a)2+a2-4a2×
,
解得:a=1或a=5,
当a=1时,b=2;当a=5时,与a+b+c=5矛盾,
则b=2.
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
又b(cosA-2cosC)=(2c-a)cosB,
∴sinB(cosA-2cosC)=(2sinC-sinA)cosB,即sinBcosA-2sinBcosC=2sinCcosB-sinAcosB,
∴sin(A+B)=2sin(B+C),即sinC=2sinA,
则c=2a,即
| c |
| a |
(Ⅱ)由(Ⅰ)∵c=2a,a+b+c=5,
∴b=5-(a+c)=5-3a,
由余弦定理得:b2=c2+a2-2accosB,
∴(5-3a)2=(2a)2+a2-4a2×
| 1 |
| 4 |
解得:a=1或a=5,
当a=1时,b=2;当a=5时,与a+b+c=5矛盾,
则b=2.
点评:此题考查了正弦、余弦定理,以及三角形的恒等变换应用,熟练掌握定理是解本题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
设a∈R,则“a=-2”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
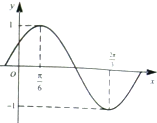 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< “开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.
“开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.  如图,设F(-c,0)是椭圆
如图,设F(-c,0)是椭圆