题目内容
10.到点F1(-1,-1)和F2(1,1)的距离之差为2$\sqrt{2}$的点的轨迹方程是y=x,(x≥1).分析 求出|F1F2|=2$\sqrt{2}$,轨迹上任意一点P有PF1-PF2=2$\sqrt{2}$=|F1F2|,由此利用双曲线定义能求出点的轨迹方程.
解答 解:∵点F1(-1,-1)和F2(1,1),
∴|F1F2|=$\sqrt{(-1-1)^{2}+(-1-1)^{2}}$=2$\sqrt{2}$,
∵动点P到点F1(-1,-1)和F2(1,1)的距离之差为2$\sqrt{2}$,
即轨迹上任意一点P有PF1-PF2=2$\sqrt{2}$=|F1F2|,
∵点F1(-1,-1)和F2(1,1)都在直线y=x上,
∴点P在直线y=x上,
又∵动点P是到F1的距离大于到F2的距离,
∴x到点F1(-1,-1)和F2(1,1)的距离之差为2$\sqrt{2}$的点的轨迹方程是y=x,(x≥1).
故答案为:y=x,(x≥1).
点评 本题考查点的轨迹方程的求法,是基础题,解题时要认真审题,注意双曲线定义的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列各式恒成立的是( )
| A. | tan$\frac{α}{2}$=$\frac{1-cosα}{sinα}$ | B. | $\frac{1+cos2α}{2}$=cos2α | ||
| C. | $\frac{2tan\frac{α}{2}}{1-ta{n}^{2}\frac{α}{2}}$=tanα | D. | ±$\sqrt{\frac{1-cosα}{1+cosα}}$=tan$\frac{α}{2}$ |
19.下列函数f(x)与g(x)是相同函数的是( )
| A. | f(x)=$\frac{x-1}{{x}^{2}-1}$,g(x)=$\frac{1}{1+x}$ | B. | f(x)=($\sqrt{x}$)2,g(x)=$\sqrt{{x}^{2}}$ | ||
| C. | f(x)=$\root{3}{{x}^{4}-{x}^{3}}$,g(x)=x$\root{3}{x-1}$ | D. | f(x)=1,g(x)=sin(arcsinx) |
18.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则( )
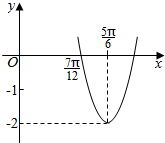

| A. | 函数f(x)在区间[0,$\frac{π}{2}$]上单调递增 | B. | 函数f(x)在区间[0,$\frac{π}{2}$]上单调递减 | ||
| C. | 函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-2 | D. | 函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-1 |