题目内容
20.求函数y=$\sqrt{2-lo{g}_{2}x}$(0$<x<\frac{1}{4}$)的值域.分析 根据对数函数的单调性根据x的范围可以求出log2x的范围,从而得出2-log2x的范围,进一步得出y的范围,即得出原函数的值域.
解答 解:∵$0<x<\frac{1}{4}$;
∴$lo{g}_{2}x<lo{g}_{2}\frac{1}{4}=-2$;
∴2-log2x>4;
∴$\sqrt{2-lo{g}_{2}x}>2$;
即y>2;
∴原函数的值域为(2,+∞).
点评 考查函数值域的概念,对数函数的单调性,根据不等式的性质求函数值域的方法.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
8.如果loga2>logb2>0,那么( )
| A. | 1<a<b | B. | 1<b<a | C. | 0<a<b<1 | D. | 0<b<a<1 |
9.已知x∈R,符号[x]表示不超过x的最大整数,若函数f(x)=$\frac{[x]}{x}$(x>0),则给出以下四个结论正确的是( )
| A. | 函数f(x)的值域为[0,1] | |
| B. | 函数f(x)的图象是一条曲线 | |
| C. | 函数f(x)是(0,+∞)上的减函数 | |
| D. | 函数g(x)=f(x)-a有且仅有3个零点时$\frac{3}{4}$<a≤$\frac{4}{5}$ |
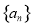 满足:①
满足:①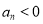 ;②
;②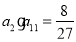 ;③
;③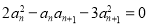 .
.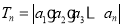 ,问:是否存在常数
,问:是否存在常数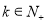 ,使得
,使得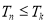 对于任意
对于任意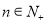 恒成立?若存在,请求出
恒成立?若存在,请求出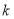 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.