题目内容
菱形 中,
中,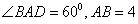 ,且
,且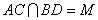 ,现将三角形
,现将三角形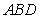 沿着
沿着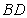 折起形成四面体
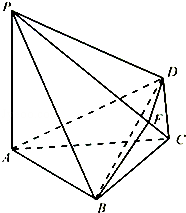
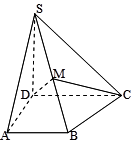
折起形成四面体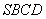 ,如图所示.
,如图所示.
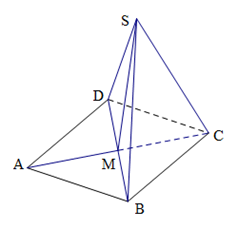
(1)当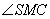 为多大时,
为多大时,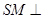 面
面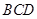 ?并证明;
?并证明;
(2)在(1)的条件下,求点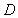 到面
到面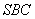 的距离.
的距离.
 中,
中,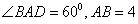 ,且
,且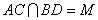 ,现将三角形
,现将三角形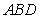 沿着
沿着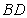 折起形成四面体
折起形成四面体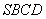 ,如图所示.
,如图所示.
(1)当
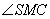 为多大时,
为多大时,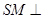 面
面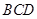 ?并证明;
?并证明;(2)在(1)的条件下,求点
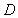 到面
到面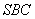 的距离.
的距离.(1)当 时,
时,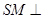 面
面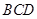 ,证明详见解析;(2)
,证明详见解析;(2) .
.
 时,
时,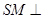 面
面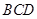 ,证明详见解析;(2)
,证明详见解析;(2) .
.试题分析:(1)根据折前四边形
 为菱形,故有
为菱形,故有 ,折后相应有
,折后相应有 ,故要使
,故要使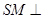 面
面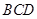 ,只须
,只须 再垂直于面
再垂直于面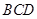 内的一条与
内的一条与 相交的直线即可,即此时
相交的直线即可,即此时 ,问题得证;(2)要求点
,问题得证;(2)要求点 到面
到面 距离,先分别计算
距离,先分别计算 、
、 ,进而根据等体积法:
,进而根据等体积法: 可求出点
可求出点 到面
到面 距离.
距离.试题解析:(1) 当
 时,
时,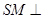 面
面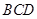
证明:此时

又因为折前四边形
 为菱形,所以
为菱形,所以 ,折后有
,折后有
 为面
为面 内两条相交直线
内两条相交直线所以
 ;
;(2)在(1)的条件下,有
 ,而
,而 ,所以三角形
,所以三角形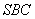 的面积为
的面积为
由等体积法可得:
 .
.
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
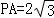 ,BC=CD=2,
,BC=CD=2,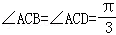 .
.
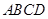 中,
中,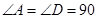 °,
°,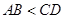 ,
,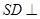 平面
平面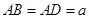 ,
,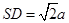 ,设
,设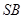 的中点为
的中点为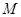 ,
,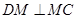 .
.
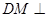 平面
平面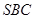 ;
;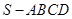 的体积.
的体积. 中,底面
中,底面 为正方形,
为正方形, 平面
平面 ,已知
,已知 ,
, 为线段
为线段 的中点.
的中点. 平面
平面 ;
;
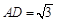 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.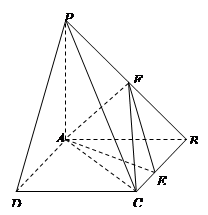
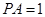 ,求证:
,求证: ;
;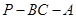 的大小为
的大小为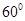 ,则CE为何值时,三棱锥
,则CE为何值时,三棱锥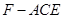 的体积为
的体积为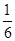 .
.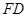 垂直于矩形
垂直于矩形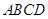 所在平面,
所在平面,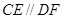 ,
,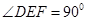 .
.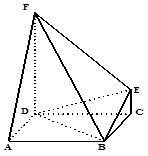
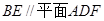 ;
;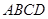 的一个边
的一个边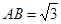 ,
,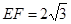 ,则另一边
,则另一边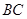 的长为何值时,三棱锥
的长为何值时,三棱锥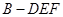 的体积为
的体积为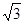 ?
? ,其底面是边长为
,其底面是边长为 的正六边形,侧棱长都相等,则该六棱锥的侧面积为 .
的正六边形,侧棱长都相等,则该六棱锥的侧面积为 .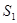 、
、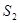 ,则
,则 的顶点都在半径为4的球
的顶点都在半径为4的球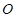 的球面上,且
的球面上,且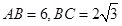 ,则棱锥
,则棱锥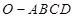 的体积为 。
的体积为 。