题目内容
如图,在直角梯形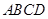 中,
中,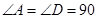 °,
°,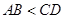 ,
,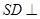 平面
平面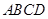 ,
,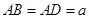 ,
,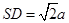 ,设
,设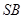 的中点为
的中点为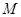 ,
,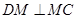 .
.
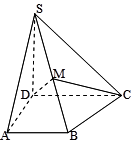
(1) 求证: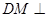 平面
平面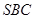 ;
;
(2) 求四棱锥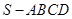 的体积.
的体积.
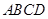 中,
中,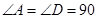 °,
°,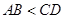 ,
,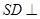 平面
平面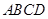 ,
,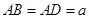 ,
,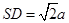 ,设
,设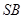 的中点为
的中点为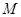 ,
,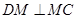 .
.
(1) 求证:
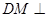 平面
平面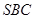 ;
;(2) 求四棱锥
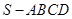 的体积.
的体积.(1)证明见解析;(2) .
.
 .
.试题分析:(1)通过勾股定理通过计算可证明
 ,然后结合条件
,然后结合条件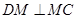 可证明得到结果;(2)首先根据条件和(1)的结论可证明
可证明得到结果;(2)首先根据条件和(1)的结论可证明 平面
平面 ,得到
,得到 ,再利用勾股定理可求得
,再利用勾股定理可求得 的值,进而求求得四棱锥
的值,进而求求得四棱锥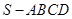 的体积.
的体积.(1)证明:
 ,
, .
.又
 ,
, .
. (2)
 ,
, .
.又
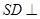 平面
平面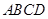 ,∴
,∴ .
.∵
 ,∴
,∴ 平面
平面 .
.∵
 平面
平面 ,∴
,∴ .
.∵


 .
. .
.∴
 .
.
练习册系列答案
相关题目
 中,
中,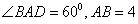 ,且
,且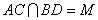 ,现将三角形
,现将三角形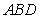 沿着
沿着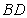 折起形成四面体
折起形成四面体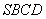 ,如图所示.
,如图所示.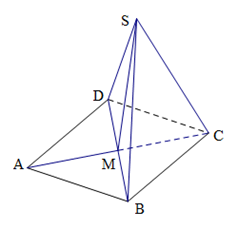
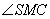 为多大时,
为多大时,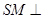 面
面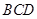 ?并证明;
?并证明;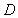 到面
到面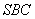 的距离.
的距离. 的底面
的底面 是边长为
是边长为 的正方形,高
的正方形,高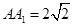 ,
, 为
为 的中点,
的中点, 与
与 交于
交于 点.
点. 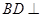 平面
平面 ;
; ∥平面
∥平面 ;
; 的体积.
的体积.
 中,侧棱
中,侧棱 平面
平面 ,
,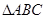 为等腰直角三角形,
为等腰直角三角形, ,且
,且 分别是
分别是 的中点.
的中点.
 平面
平面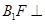 平面
平面 ;
; ,求三棱锥
,求三棱锥 的体积.
的体积. 时,则该圆锥体的体积是 .
时,则该圆锥体的体积是 . ,它的三视图中的俯视图如图所示,侧视图是一个矩形,则这个矩形的面积是( )
,它的三视图中的俯视图如图所示,侧视图是一个矩形,则这个矩形的面积是( )
 ,那么正方体的棱长等于( )
,那么正方体的棱长等于( )



