题目内容
如图,在四棱锥P-ABCD中,底面ABCD是正方形,
侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
⑴求证:PA∥平面BDE;
⑵求证:平面BDE⊥平面PBC.
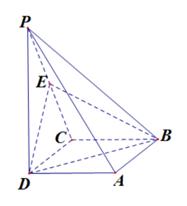 |
⑴连接AC,设AC与BD的交点为O,连接OE.
 ∵在△PCA中,OE是△PCA的中位线,∴PA∥OE.
∵在△PCA中,OE是△PCA的中位线,∴PA∥OE.
又PA不在平面BDE内,∴PA∥平面BDE.
⑵∵PD⊥底面ABCD。∴CB⊥PD.
又BC⊥DC, ∴BC⊥平面PDC.
∴BC⊥平面PDC.
 ,∴DE⊥BC
,∴DE⊥BC
在△PDC中,PD=DC,E是PC的中点,∴DE⊥PC.
 因此有DE⊥平面PBC.
因此有DE⊥平面PBC.
∵DE 平面BDE,∴平面BDE⊥平面PBC.
平面BDE,∴平面BDE⊥平面PBC.

练习册系列答案
相关题目
 ,
, ,求a的取值范围.
,求a的取值范围.

 在点
在点 处的切线方程为________.
处的切线方程为________.  如图在
如图在 中,AB=AC,过点A的直线与
中,AB=AC,过点A的直线与
 ={1,2,3,4,5},
={1,2,3,4,5}, ={2,4},则
={2,4},则 = .
= . 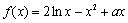 (
(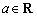 ).
).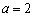 时,求
时,求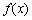 的图象在
的图象在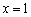 处的切线方程;
处的切线方程;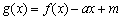 在
在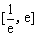 上有两个零点,求实数
上有两个零点,求实数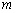 的取值范围;
的取值范围;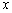 轴有两个不同的交点
轴有两个不同的交点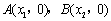 ,且
,且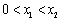 ,
,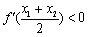 (其中
(其中 是
是 是定义在R上的奇函数,又是周期为2的周期函数,当
是定义在R上的奇函数,又是周期为2的周期函数,当 时,
时,  ,则
,则 的值为_____.
的值为_____.