题目内容
3.关于x的不等式x2-x+a<0的解集为空集,则实数a的取值范围为a≥$\frac{1}{4}$.分析 根据关于x的不等式x2-x+a<0的解集为空集,△≤0,解不等式即可.
解答 解:关于x的不等式x2-x+a<0的解集为空集,
∴△=1-4a≤0,
解得a≥$\frac{1}{4}$;
∴实数a的取值范围是a≥$\frac{1}{4}$.
故答案为:a≥$\frac{1}{4}$.
点评 本题考查了一元二次不等式的解法与应用问题,是基础题.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
18.函数f(x)=(x+1)2-2x的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
5.椭圆b2x2+a2y2=1(a>b>0)的左焦点为F,右顶点为A,上顶点为B,若∠ABF=90°,则椭圆的离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
9.在正方体ABCD-A1B1C1D1中,过AC与BD1平行的平面必过( )
| A. | DD1的中点 | B. | DD1的三等分点 | C. | D1C1的中点 | D. | A1D1的中点 |
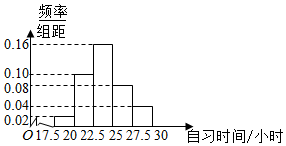 某高校为调查1000名学生每周的自习时间(单位:小时),从中随机抽查了100名学生每周的自习时间,制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,估计这1000名学生中每周的自习时间不少于22.5小时的人数是700.
某高校为调查1000名学生每周的自习时间(单位:小时),从中随机抽查了100名学生每周的自习时间,制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,估计这1000名学生中每周的自习时间不少于22.5小时的人数是700.