题目内容
14.在三棱锥S-ABC内任取一点P,使得VP-ABC>$\frac{1}{2}$VS-ABC的概率是$\frac{1}{8}$.分析 取高线的中点,过该点作平行于底的平面,根据条件关系得到P满足的条件,根据概率为小棱锥与原棱锥体积之比,用相似比计算即可.
解答 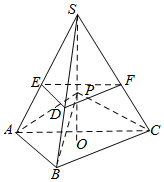 解:作出S在底面△ABC的射影为O,
解:作出S在底面△ABC的射影为O,
若VP-ABC=$\frac{1}{2}$VS-ABC,则高OP=$\frac{1}{2}$SO,
即此时P在三棱锥VS-ABC的中垂面DEF上,
则VP-ABC>$\frac{1}{2}$VS-ABC的点P位于小三棱锥VS-EDF内,
则对应的概率P=($\frac{1}{2}$)3=$\frac{1}{8}$,
故答案为:$\frac{1}{8}$.
点评 本题主要考查几何概型的概率计算,求出对应的体积关系是解决本题的关键,根据比例关系,得到面积之比是相似比的平方,体积之比是相似比的立方.

练习册系列答案
相关题目
8.已知sin(π-α)=-2sin($\frac{π}{2}$+α),则tanα的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
2.从集合A={-1,$\frac{1}{2}$,2}中随机选取一个数记为k,从集合B={$\frac{1}{2}$,$\frac{3}{2}$,2}中随机选取一个数记为a,则ak>1的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{9}$ | D. | $\frac{5}{9}$ |
9.(1+2x)3(1-x)4展开式中x项的系数为( )
| A. | 10 | B. | -10 | C. | 2 | D. | -2 |
6.下列关于空间的直线和平面的叙述,正确的是( )
| A. | 平行于同一平面的两直线平行 | |
| B. | 垂直于同一平面的两平面平行 | |
| C. | 如果两条互相垂直的直线都分别平行于两个不同的平面,那么这两个平面平行 | |
| D. | 如果一个平面内一条直线垂直于另一个平面的一条垂线,那么这两个平面垂直 |
4.设Sn为等比数列{an}的 前n项和,a2-8a5=0,则$\frac{{S}_{8}}{{S}_{4}}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{17}{16}$ | C. | 2 | D. | 17 |



